Немного про график параболы Как решать 10-ю задачу ЕГЭ 2023.

Как решать 10-ю задачу ЕГЭ 2023.

Еще одна задача с параметрами, когда то ее решали на факультете почвоведения. Вот она там последняя.

Будет немного Решений..

Пример вычисления определителей методом рекурентных соотношений.

Пример вычисления определителя методом выделения линейных множителей.

Матричная экспонента.

Возвести экспоненту в матричную степень, т.е. найти 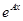, где 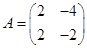. Случай комплексных собственных значений.
План: Найдем частные решения системы 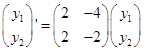при начальных условиях : 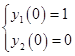и 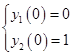и искомая матричная экспонента будет матрицей, где эти частные решения будут записаны по столбцам.
Решение:
Для начала, найдем собственные значения этой матрицы:

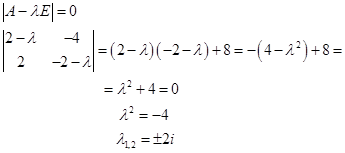
Теперь найдем собственные вектора:
1)

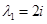
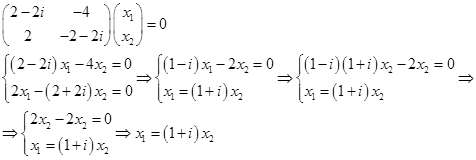
Тогда за собственный вектор в этом случае возьмем:

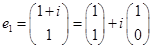
Второй собственный вектор нам в этом случае без надобности, все равно там все сопряженное. Продолжим.


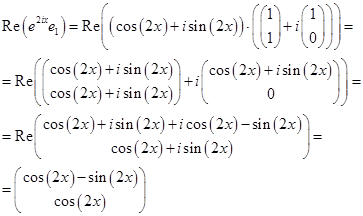
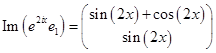
Тогда, общим решением системы дифференциальных уравнений

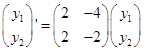
Будет: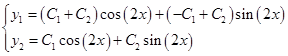
И найдем частное решение при начальных условиях: 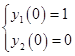и .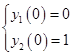
1) 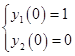, подставим в общее решение:

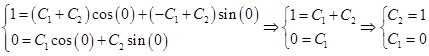
И частное решение примет вид: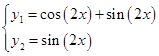

2) 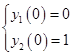, подставим в общее решение:

И частное решение примет вид:

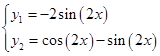
Запишем эти частные решения по столбцам:

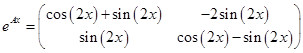
Проверку можно сделать при помощи математического пакета Maple, т.е. вычислить в Мапле матричную экспоненту.
Следует для начала подключить библиотеку функций для линейно алгебры:
>with(linalg);
И потом вот такое написать:
>exponential( 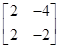,x);
Мапле выдаст вам такое:

Что совпадает с нашим ответом.

Случай трех переменных.

Много сегодня:
5. Построение графика модуля функции.
6. Решение уравнений с модулем графическим методом.
7. Решение неравенства с модулем графическим методом.