Задача. Пусть производство продукции осуществляется на 4-х предприятиях А₁, А₂, А₃, А₄ а затем развозится в 5 пунктов потребления этой продукции B₁, B₂, B₃, B₄, B₅. На предприятиях A_i (i = 1, 2, 3, 4) продукция находится соответственно в количествах a_i (условных единиц). В пункты B_j (j = 1, 2, 3, 4,5) требуется доставить b_j единиц продукции. Стоимость перевозки единицы груза (с учетом расстояний) из A_i в B_j определена матрицей .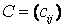
Предприятия могут выпускать в день 235, 175, 185 и 175 единиц продукции. Пункты потребления готовы принимать ежедневно 125, 160, 60, 250 и 175 единиц продукции. Стоимость перевозки единицы продукции (в у. е.) с предприятий в пункты потребления приведена в таблице.

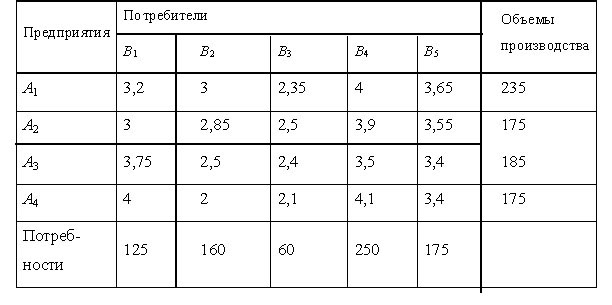
Требуется минимизировать суммарные транспортные расходы по перевозке продукции.

Решение.
Необходимо выполнить следующее:
1. Установить, является ли модель транспортной задачи, заданная таблицей, сбалансированной.
2. Разработать математическую модель задачи.
3. Найти минимальную стоимость перевозок, используя надстройку «Поиск решения» в среде MS Excel.

Решение.

1. Выполним проверку сбалансированности математической модели задачи. Модель является сбалансированной, так как суммарный объем производимой продукции в день равен суммарному объему потребности в ней:

235+175+185+175=125+160+60+250+175

(При решении этой задачи не учитываются издержки, связанные со складированием и недопоставкой продукции).

2. Приступим к построению математической модели поставленной задачи. Неизвестными будем считать объемы перевозок.
Пусть х_ij – объем перевозок с i-го пункта поставки в j-й пункт потребления. Суммарные транспортные расходы – это функция 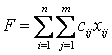, где с_ij – стоимость перевозки единицы продукции с i-го предприятия в j-й пункт потребления .

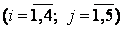Неизвестные в этой задаче должны удовлетворять следующим ограничениям:
• Объемы перевозок не могут быть отрицательными, т. е. ;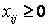
• Поскольку модель сбалансирована, то вся продукция должна быть вывезена с предприятий, а потребности всех пунктов потребления должны быть полностью удовлетворены, т. е. 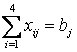и .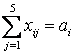

Итак, имеем следующую задачу ЛП:
найти минимум функции: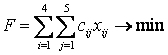
при ограничениях:


, ,

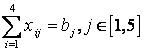
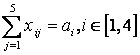
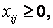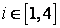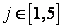
3. Приступаем к решению задачи на компьютере.
3.1. Откроем новый рабочий лист Excel.
3.2. В ячейки B3:F6 стоимость перевозок единицы груза.
3.3. В ячейках B16:F16 укажем формулы для расчета суммарной потребности продукции для j-го пункта, в ячейках G12:G15 – формулы суммарного объема производства i-го предприятия.

3.4. В ячейки B18:F18 заносим значения потребности продукции соответствующего пункта потребления, в ячейки H12:H15 заносим значения объема производства соответствующего предприятия.
3.5. В ячейку B20 занесем формулу целевой функции.
3.6. Выполним команду Сервис → Поиск решения. Откроется диалоговое окно Поиск решения. Если такой команды во вкладке Сервис нет, то следует подключить эту надстройку перейдя по Сервис → Надстройки, и поставив галочку напротив нужной, т.е. Поиск решения.
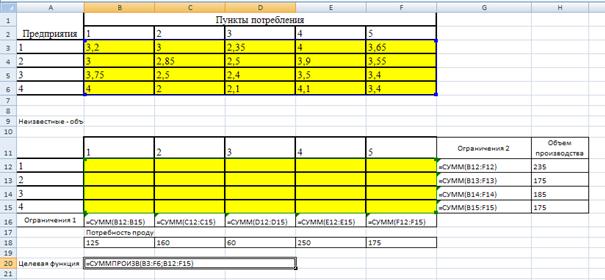
3.7. В поле Установить целевую ячейку указываем ячейку, содержащую оптимизируемое значение. Установим переключатель Равный в положение минимальному значению.
3.8. В поле Изменяя ячейки мышью зададим диапазон подбираемых параметров $B$12:$F$15.
3.9. В поле Ограничения введем необходимые ограничения и нажмем на кнопку Добавить, затем Выполнить.

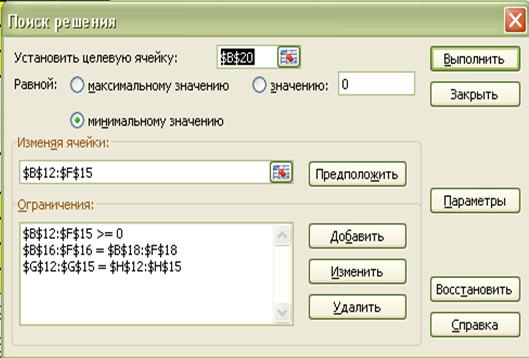
В результате получится оптимальный набор переменных при данных ограничениях:

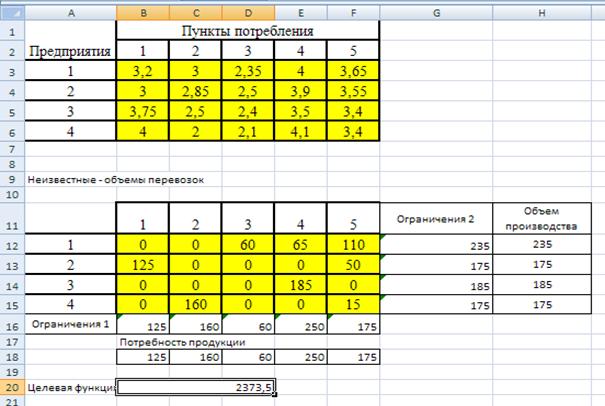
Оптимальность решения можно проверить, экспериментируя со значениями ячеек $B$12:$F$15.