Метод неопределенных коэффициентов есть разложение правильных дробей на сумму нескольких.
Например, с помощью этого метода дробь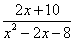 
можно записать в виде:
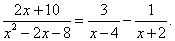
Напомним определение правильной дроби.
Пусть дана некоторая функция вида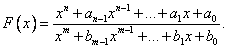 
Если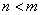 
, то данная функция является правильной дробью. Соответственно, если 
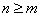, то функция называется неправильной дробью. Если дробь неправильная, нужно выделить в ней целую часть, разделив уголком числитель на знаменатель.
Теорема.
Каждая правильная дробь может быть единственным образом представлена в виде суммы простых дробей.
Существует несколько видов разложения дроби на простые в зависимости от вида дроби. Рассмотрим их на примерах.
Пример 1.
Правильная дробь вида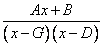 
(в числителе стоит линейное выражение, в знаменателе – многочлен второй степени, знаменатель уже разложен на множители).
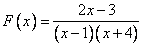
Представим данную дробь в виде суммы двух дробей со знаменателями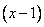 
и 
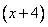. Мы выбрали именно эти знаменатели, так как числитель исходной дроби был разложен на такие сомножители. Числителями данных дробей будут служить неизвестные коэффициенты E и F, которые нам предстоит найти. Отсюда и название метода – метод неопределенных коэффициентов.
В числителях новых дробей нужно ставить общий вид многочлена степени на единицу меньше знаменателя. Степень знаменателе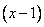й и 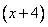равна единице, значит степень числителей должна быль равна нулю. Так как число- многочлен нулевой степени, то разложение будет выглядеть вот так:
.
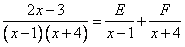Приводим дроби к общему знаменателю и группируем относительно степеней:
.
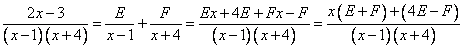То есть, получили что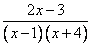 
= 
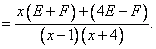
Тогда должно выполняться равенство числителей: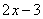 
=
.
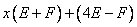В левой части равенства перед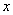 
стоит коэффициент 2, а в правой части перед 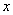стоит коэффициент 
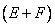. Приравниваем их, то же делаем и для оставшихся частей равенства: (-3) должно быть равно 
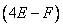, чтобы равенство выполнялось.
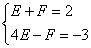
Это линейная система уравнений с двумя неизвестными. Выразим из первого уравнения любое неизвестное и подставим во второе.
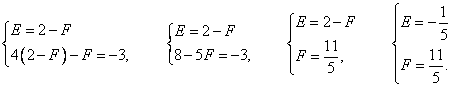
Таким образом, мы нашли нужные коэффициенты и теперь можем поставить их обратно в разложение дроби:
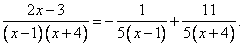
Пример 2. (Правильная дробь вида 
, числитель – линейный, а знаменатель как минимум имеет третью степень).
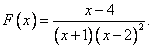
Смотрим на знаменатель дроби и размышляем о степенях числителей в разложении. Первый сомножитель в знаменателе – это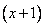 
, значит, степень числителя дроби с таким знаменателем будет равна нулю. Иначе говоря, числителем будет просто число. Второй сомножитель в знаменателе дроби есть 
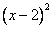(степень здесь равна двум), поэтому числителем будет многочлен общего вида степени на единицу меньше, т.е., например, 
.
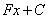Запишем это:
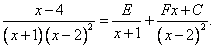
Как и ранее, приводим дробь к общему знаменателю и группируем числитель относительно степеней :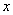
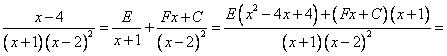
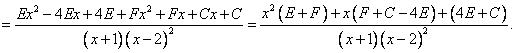
Смотрим на первую и последнюю дроби в данном равенстве.
Получаем, что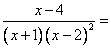 
=
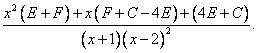
Тогда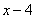 
=
.
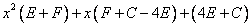В левой части равенства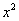 
отсутствует, а в правой – нет. Чтобы равенство числителей выполнялось, нужно взять коэффициент, стоящий в правой части перед 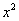и приравнять его к нулю. 
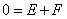. Далее, разбираемся с коэффициентом при : 
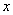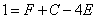, так как 
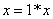для левой части равенства. Свободные члены приравниваем так, как есть:
-4 =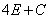 
.
Записываем все полученное и получаем систему уравнений
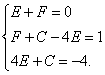
Выразим в системе из первого уравнения переменную F, подставим ее во второе уравнение и вычтем из третьего уравнения второе.
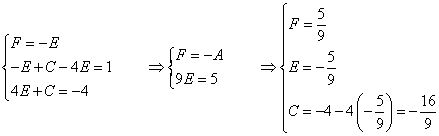
Возвращаемся к началу задачи и подставляем полученные коэффициенты в разложение.
Пример 3. (Дробь правильная, но знаменатель не разложен на множители).
.
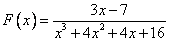Рассмотрим знаменатель дроби отдельно.
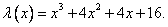Разложим данную функцию на множители группировкой:
.
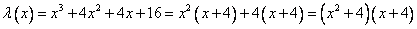Теперь, когда знаменатель разложен на множители, запишем исходную дробь в новом виде и применим все тот же метод неопределенных коэффициентов.
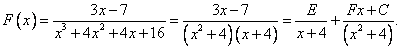
Приводим дроби к общему знаменателю и группируем коэффициенты при степенях неизвестной.
.
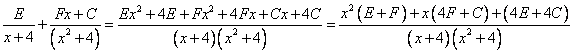Приравниваем новую и старую дроби:
= .
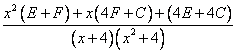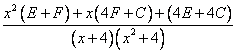Тогда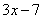 
=
.
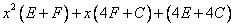Составляем систему уравнений:
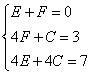
Выразим из первого уравнения переменную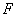 
, подставим ее во второе уравнение и сложим второе и третье уравнения.
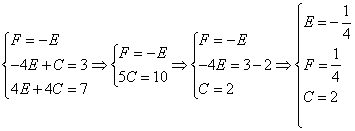
Легким движением руки решили систему. Записываем ответ.
=
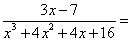Пример 4.
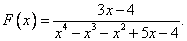
Также, как и в предыдущем примере, разложим знаменатель на сомножители.
=
.
=
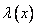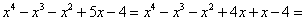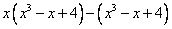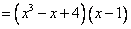
Заметим, что кубический трехчлен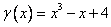 
имеет лишь один действительный корень, поэтому его на множители раскладывать мы не будем, вместо этого разложим исходную дробь следующим образом:
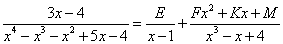
В этом есть отличие данного примера от предыдущего. Числитель второй дроби записываем в общем виде квадратного трехчлена, так как степень знаменателя равна тройке.
=
.
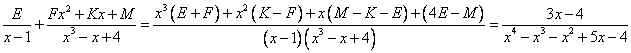
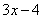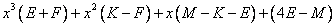Составляем систему уравнений:
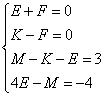
Сложим первое и второе уравнения:
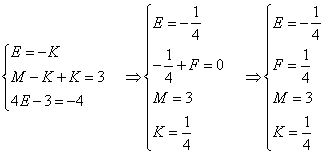
Подставляем полученные коэффициенты в дробь.
.
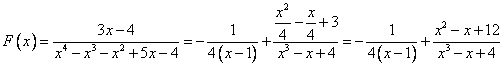Подведем итог всему вышесказанному.
Если стоит задача разложить дробь на простейшие, то :
1) В первую очередь убедитесь, что она правильная. ( не задача, а дробь). Если дробь неправильная- делением разложить ее на правильную дробь и многочлен.
2)Удостоверившись, что мы имеем дело с правильной дробью, смотрим на ее знаменатель. Если он еще не разложен на множители – раскладываем.
3)Применяем метод неопределенных коэффициентов: в зависимости от вида знаменателя, раскладываем дробь на сумму дробей, которые будут зависеть от вида знаменателя исходной дроби. Составляем систему.
4) Решаем полученную систему, находим коэффициенты, подставляем их в разложение дроби.
5)Записываем ответ.
Замечание: Коэффициенты и числители при разложении дроби на сумму нескольких зависят от конкретного вида дроби, а точнее ее знаменателя, главное, чтоб дробь была правильной.