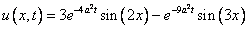Решить начально-краевую задачу для однородного уравнения теплопроводности

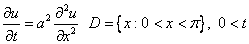
С однородными граничными условиями и заданным начальным условием


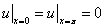
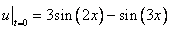
Решение:
Сначала решим задачу Штурма-Лиувилля,

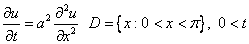
С однородными граничными условиями

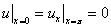
методом разделения переменных.
Будем искать частные решения однородного уравнения, удовлетворяющие однородным граничным условиям в виде

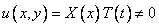
Поставим это выражение в исходное уравнение

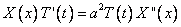
И разделим переменные

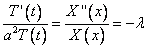
Получим дифференциальные уравнения

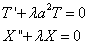
Подставим граничные условия

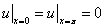
в выражение

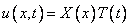
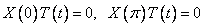
Т.к. 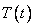тождественно не равны нулю, то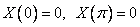

Решение задачи Штурма-Лиувилля: собственные значения и соответствующие им собственные функции при 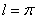имеют следующий вид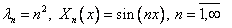

Рассмотрим уравнение
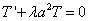
при

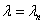
При 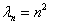общее решение можно записать в виде:

.
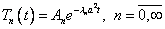На данный момент найдено множество счетных решений

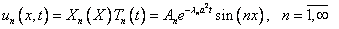
А решение всей задачи будем искать в виде функционального ряда
,
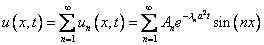предполагая, что его можно дважды дифференцировать по переменной х и один раз по переменной t.
Поставим в это решение для определения коэффициентов начальное условие

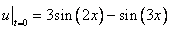
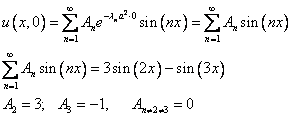
Подставим коэффициенты и получим
Ответ: