По данным, приведенным в таблице:
1) Построить линейное уравнение парной регрессии y на x;
2) Рассчитать линейный коэффициент парной корреляции и оценить тесноту связи;
3) Оценить статистическую значимость параметров регрессии и корреляции, используя F-статистику, t-статистику Стьюдента и путем расчета доверительных интервалов каждого из показателей;
4) Вычислить прогнозное значение y при прогнозном значении x, составляющем 108% от среднего уровня;
5) Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал;
6) Полученные результаты изобразить графически и провести экономическое обоснование.
В таблице приведены данные, отражающие зависимость между количеством этажей жилого дома x(шт.) и временем строительства y (мес.) у 10 строительных компаний.
Решение.
1. Заполним таблицу экспериментальных данных, за исключением двух последних столбцов.
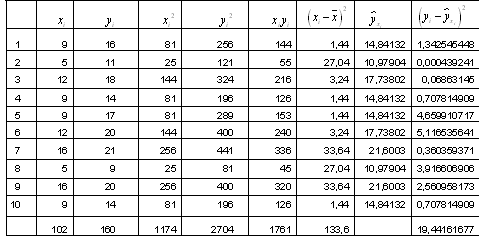
Найдем параметры линейной регрессии
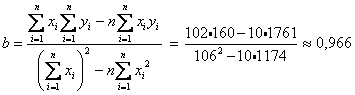
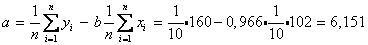
Следовательно, уравнение регрессии имеет вид
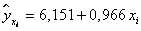
Значит, при увеличении количества этажей на 1 срок постройки дома увеличится в среднем на 0,966 месяца.
С помощью найденного уравнения регрессии заполняем два последних столбика таблицы, учитывая, что среднее значение независимой переменной
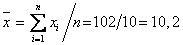
2. Рассчитаем линейный коэффициент парной корреляции
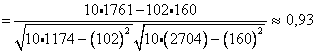
Связь очень хорошая.
3. Используя данные из таблицы, найдем интервальные оценки параметров регрессии с 95% надежностью.
Стандартная ошибка оценки равна
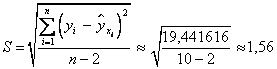
Интервал для свободного члена регрессии (параметра А)
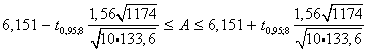
Коэффициент Стьюдента
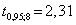, следовательно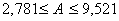
Интервальная оценка для коэффициента регрессии
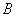определяется по следующей формуле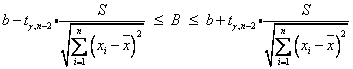
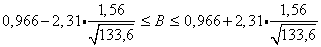
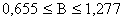
Т.е. с надежностью 0,95 при увеличении количества этажей в доме на 1, время строительства дома увеличивается в среднем на величину, заключенную в пределах от 0,655 до 1,277.
Оценим значимость коэффициентов регрессии и корреляции с помощью t-статистики Стьюдента. Для этого необходимо сравнить табличное значение t-критерия (для уровня значимость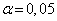 
и числа степеней свободы 
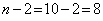) с расчетными критериями 
:
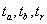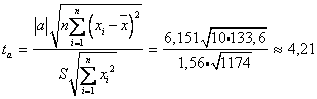
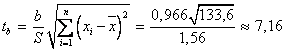
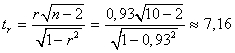
Коэффициент Стьюдента
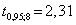, следовательно, фактические значения 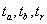не превосходят табличное значение
; 
; 
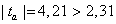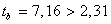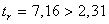
И коэффициенты
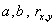значимы.
4) Вычислим прогнозное значение y при прогнозном значении x, составляющем 108% от среднего уровня.
, 
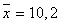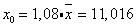
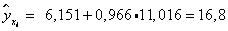
5) Оценим точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.
Индивидуальные значения урожайности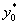 
принадлежат промежутку
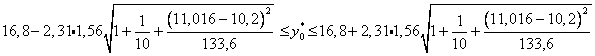
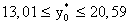
6) Нанесем экспериментальные точки на координатную плоскость, построим уравнение регрессии (точки – наблюдаемые значения, прямая – линия регрессии)
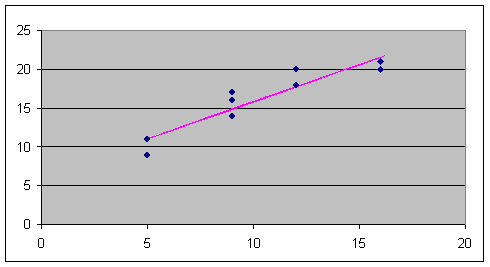
Можно сделать вывод о правомочности применения линейной регрессионной модели.