Задача: Отделить один корень уравнения 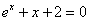и вычислить его на полученном отрезке [a;b] с точностью до 0,0001 тремя методами.
А) метод дихотомии
Б) метод простой итерации.
Г) метод хорд.

Решение:
а) решить уравнение методом простой итерации
Отделим корень, для этого преобразуем уравнение к виду:

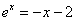
и построим графики функций , .

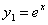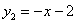Пересечение этих графиков видно на интервале [-3;-2], т.е. корень будем искать именно на этом промежутке.

Преобразуем уравнение к виду

.
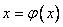
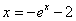Выберем первое приближение .


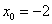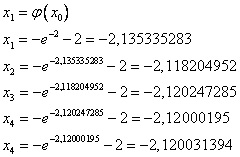
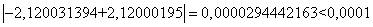
т.о., с требуемой точностью

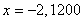
Ответ:

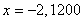
б) решим уравнение методом дихотомии (деление отрезка, на котором отделен корень, пополам).
Уравнение:
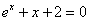
Отрезок, на котором будем искать корень [-3;-2].

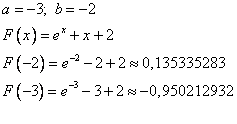
на концах отрезка функция принимает разные знаки

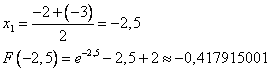
Рассмотрим отрезок [-2,5;-2], т.к. на его концах функция принимает разные по знаку значения.

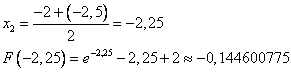
Рассмотрим отрезок [-2,25;-2], т.к. на его концах функция принимает разные по знаку значения.

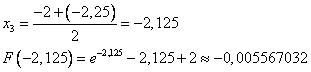
Рассмотрим отрезок [-2,125;-2], т.к. на его концах функция принимает разные по знаку значения.

Рассмотрим отрезок [-2,125;-2,0625], т.к. на его концах функция принимает разные по знаку значения.

Рассмотрим отрезок [-2,125;-2,09375], т.к. на его концах функция принимает разные по знаку значения.

Рассмотрим отрезок [-2,125;-2,109375], т.к. на его концах функция принимает разные по знаку значения.

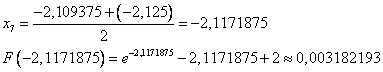
Рассмотрим отрезок [-2,125;-2,1171875], т.к. на его концах функция принимает разные по знаку значения.

Рассмотрим отрезок [-2,12109375;-2,1171875], т.к. на его концах функция принимает разные по знаку значения.

Рассмотрим отрезок [-2,12109375;-2,119140625], т.к. на его концах функция принимает разные по знаку значения.

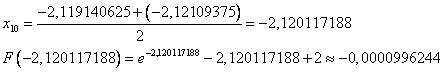
Т.к. 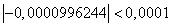, то корень найден с заданной точностью

Ответ: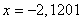

Г) решить уравнение методом хорд.
Уравнение: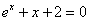
Итерационная формула имеет вид:

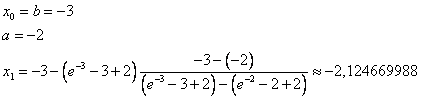
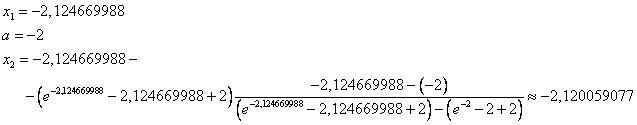
Корень найден с заданной точностью

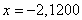
Ответ:

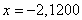
Вывод:
При решении этого уравнения тремя способами получены корни:



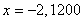
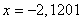
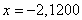
Значение функции Уравнение: 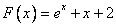в этих точках соответственно равно
0,00003163
-0,00008037

Т.е. очень не значимо отличается от нуля. Различия в значении корней в первом, втором и третьем случае объясняется различными критериями остановки итерационного процесса

Понравилась статья?