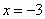Задача: Дан график производной функции 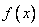. Определить, в какой точке отрезка 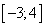функция принимает наибольшее значение.

Решение:

Отбросим лишнее (оставим на чертеже только отрезок )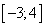

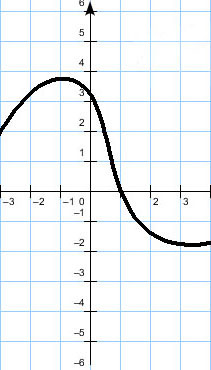
Требуется определить точку, в которой функция принимает наибольшее значение.

Вспомним статью: Нахождение максимума и минимума функции одной переменной..

Замечание 1: Вторая теорема Вейерштрасса: функция, непрерывная на отрезке, принимает на нем наибольшее и наименьшее значения.

Замечание 2: Это наибольшее и наименьшее значение она достигает или внутри отрезка или на его границах.

Замечание 3: В точке максимума производная функции равна нулю и меняет свой знак с плюса на минус.

В этом случае есть две точки, в которых производная равна нулю, но только при 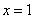этот график переходит из верхней полуплоскости в нижнюю (т.е. производная меняет свой знак с «+» на «-»).

Вывод: — точка максимума функции 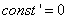на отрезке .

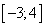Ответ: в точке 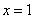функция достигает своего наибольшего значения на отрезке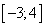

Замечание:

А зачем, собственно говоря, в условии задачи дано ограничение на рассматриваемый отрезок? И почему именно ?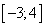
Рассмотрим и проанализируем отрезок .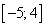

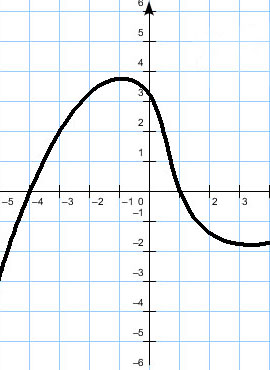
1) на интервале 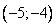производная (а это график производной 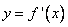) отрицательна, т.е. функция 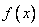убывает .

2) в точке 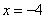производная равна 0 и меняет свой знак с «-» на «+», т.е. функция 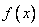имеет в этой точке минимум.

3) на интервале 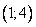производная 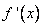положительна (график лежит выше оси ОХ) , т.е. функция 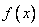возрастает.

4) в точке 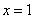производная равна 0 и меняет свой знак с «+» на «-», т.е. функция 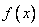имеет в этой точке максимум.

5) на отрезке 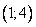производная отрицательна, т.е. функция 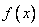убывает.

Построим пример графика, удовлетворяющий пунктам 1) — 6).

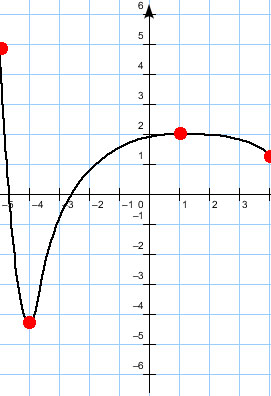
В данном случае наибольшее значение функция принимает наибольшее значение на границе интервала в точке 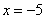, а не в точке максимума .

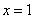Только по графику производной сравнивать значение функции практически невозможно, поэтому и взят интервал 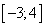, на котором функция сначала возрастает, а потом убывает, т.е. думать особо не надо.

Задача: Дан график производной функции 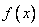. Определить, в какой точке отрезка 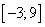функция принимает наибольшее значение.

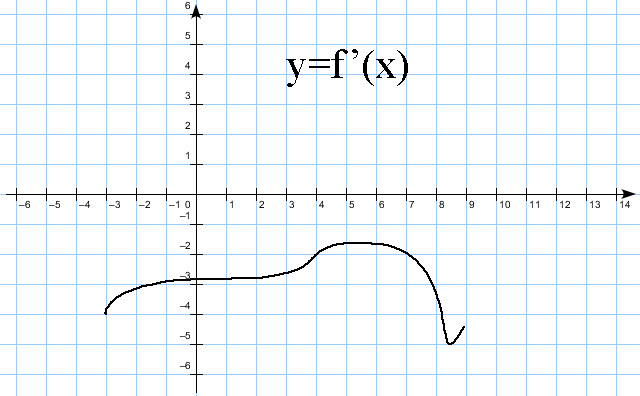
Решение:

Замечание: дан график ПРОИЗВОДНОЙ!!!

На рассматриваемом отрезке производная всюду отрицательна (лежит ниже оси ОХ ), т.е. функция всюду убывает на этом отрезке, типа вот такого:

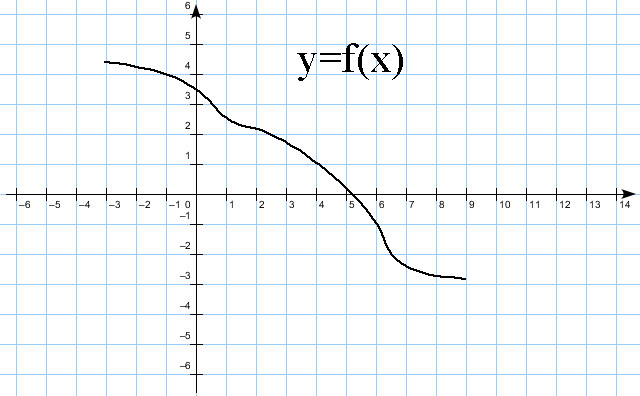
Очевидно, что наибольшее значение функция принимает в левой точке рассматриваемого отрезка.

Ответ: Функция 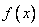, определенная на отрезке 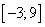принимает наибольшее значение в точке