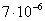Задача: Найти четыре первых, отличных от нуля члена разложения в ряд частного решения дифференциального уравнения, удовлетворяющего заданным начальным условиям и проверить это решение при помощи метода Пикара. Оценить точность при применении метода Пикара.
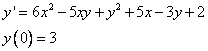
Решение: 1) найдем 4 отличные от нуля члена разложения решения в ряд.
Пусть функция 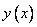 является решением этого уравнения с начальным условием. Разложение этой функции в ряд в окрестности точки 0 имеет вид.
является решением этого уравнения с начальным условием. Разложение этой функции в ряд в окрестности точки 0 имеет вид.
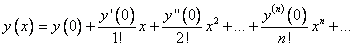
По условию: 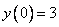
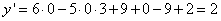
Найдем 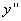
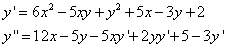
Найдем 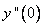 при том, что
при том, что 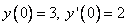
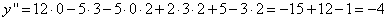
Т.е. 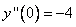 .
.
Найдем 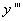
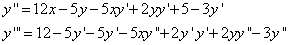
Найдем 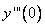 при том, что
при том, что 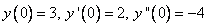
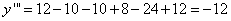
Т.е. 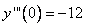 .
.
Составим разложение в ряд:

Для проверки воспользуемся формулой
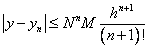
т.к. неявно заданная функция 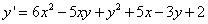 определена и непрерывна на во всей плоскости, то возьмем любой интервал, например
определена и непрерывна на во всей плоскости, то возьмем любой интервал, например 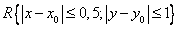
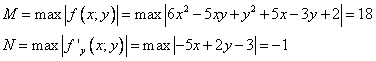
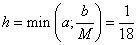
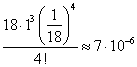
Ответ: 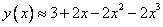 , ошибка составляет не более
, ошибка составляет не более