По данным определить наличие и направление связи между признаками, построить уравнение регрессии. Построить график теоретического и практического значения Y.
| Домашние хозяйства, проживаю-щие в жилище, оборудованном: | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 |
| Водопроводом Х | 84,6 | 84,5 | 85,4 | 86,2 | 87,4 | 88 | 88 | 88,3 | 89 | 90,3 |
| Канализацией У | 81,2 | 79,8 | 80,5 | 81,4 | 78,3 | 77,8 | 77,7 | 75,5 | 75,8 | 76,3 |
Решение:
1) Определить наличие и направление связи между признаками.
Построим поле корреляции:
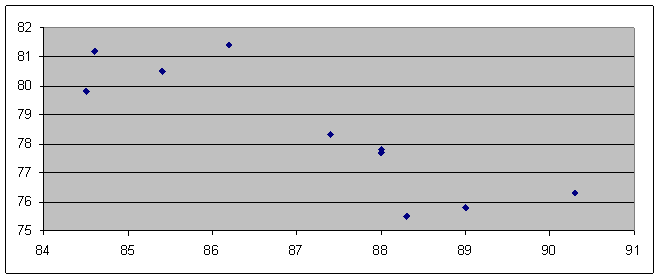
Сделаем предположение, что связь есть, направление связи – обратное.
2) построить уравнение регрессии.
Для построение уравнения линейной регрессии вида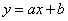 
используем метод наименьших квадратов.
Составим систему нормальных уравнений
Для вычисления коэффициентов системы составим вспомогательную таблицу:
| x | y | x^2 | xy | Y^2 | |
| 84,6 | 81,2 | 7157,16 | 6869,52 | 6593,44 | |
| 84,5 | 79,8 | 7140,25 | 6743,1 | 6368,04 | |
| 85,4 | 80,5 | 7293,16 | 6874,7 | 6480,25 | |
| 86,2 | 81,4 | 7430,44 | 7016,68 | 6625,96 | |
| 87,4 | 78,3 | 7638,76 | 6843,42 | 6130,89 | |
| 88 | 77,8 | 7744 | 6846,4 | 6052,84 | |
| 88 | 77,7 | 7744 | 6837,6 | 6037,29 | |
| 88,3 | 75,5 | 7796,89 | 6666,65 | 5700,25 | |
| 89 | 75,8 | 7921 | 6746,2 | 5745,64 | |
| 90,3 | 76,3 | 8154,09 | 6889,89 | 5821,69 | |
| СУММА: | 871,7 | 784,3 | 76019,75 | 68334,16 | 61556,29 |
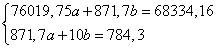
Решим эту систему методом Крамера:
Уравнение регрессии имеет вид:
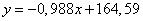
3) Проверить надёжность его параметров и надёжность коэффициента корреляции.
Рассчитаем коэффициент корреляции
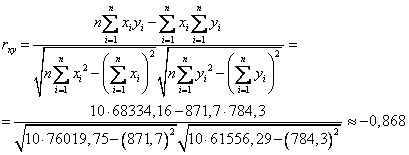
Построим график теоретических и практических значений Y.
Заполним столбец теоретических значений Y используя уравнение регрессии:
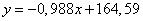
| x | y | x^2 |
| 84,6 | 81,2 | 80,97 |
| 84,5 | 79,8 | 81,07 |
| 85,4 | 80,5 | 80,18 |
| 86,2 | 81,4 | 79,39 |
| 87,4 | 78,3 | 78,20 |
| 88 | 77,8 | 77,61 |
| 88 | 77,7 | 77,61 |
| 88,3 | 75,5 | 77,31 |
| 89 | 75,8 | 76,62 |
| 90,3 | 76,3 | 75,34 |
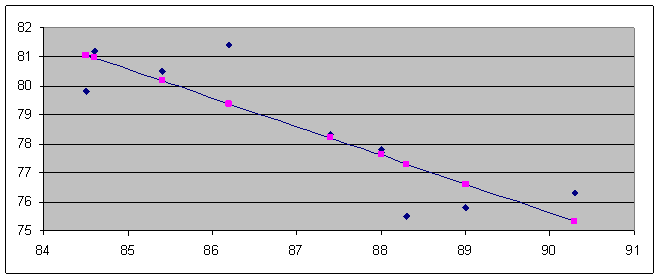
Теоретические значения соединены линией.