Проведено 100 независимых измерений значений непрерывной случайной величины X. Результаты измерений оформлены в виде статистической совокупности
| -7 | -12 | 6 | -9 | -4 | 17 | 1 | -3 | -9 | -3 |
| 3 | -5 | 9 | 15 | -2 | 20 | 14 | 11 | 1 | 11 |
| -1 | -4 | 14 | 6 | 8 | -5 | -19 | -3 | -4 | 5 |
| -1 | -21 | 4 | 3 | 13 | 18 | -8 | 11 | -12 | -15 |
| 6 | 6 | 14 | -5 | -3 | 1 | -13 | -2 | 15 | -8 |
| 9 | 19 | 6 | 2 | -18 | 9 | 12 | 2 | 14 | 2 |
| 12 | 7 | 10 | 1 | -5 | 2 | 4 | -13 | -12 | -15 |
| 17 | -4 | -8 | 14 | 16 | 1 | 28 | 2 | -1 | 8 |
| 1 | -5 | 7 | -9 | -5 | -17 | 17 | 0 | 7 | 9 |
| -8 | -3 | 4 | -11 | -4 | 3 | -8 | -21 | 4 | 6 |
Выполнить статистическую обработку этих данных.
Для этого необходимо:
1) записать вариационный ряд (первая строка – варианты, вторая – соответствующие им частоты);
2) записать статистический закон распределения случайной величины X.
3) найти несмещенные оценки математического ожидания и дисперсии случайной величины X.
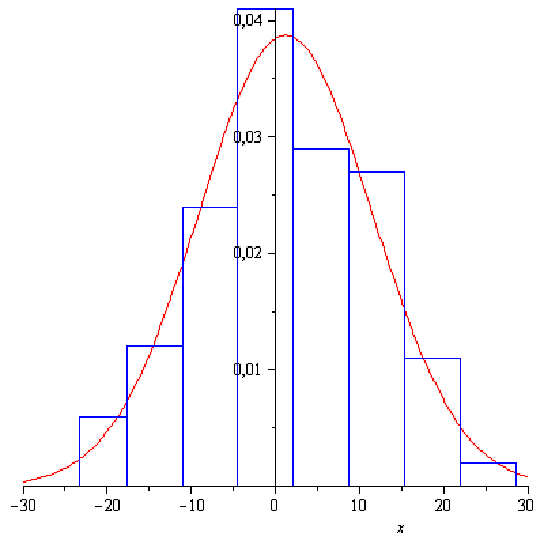
4) построить гистограмму относительных частот;
5) при уровне значимости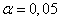 
проверить по критерию согласия Пирсона нулевую гипотезу о том, что случайная величина X имеет нормальное распределение;
6) если нулевая гипотеза о нормальном распределении случайной величины X принимается, то построить кривую нормального распределения на одном рисунке с гистограммой относительных частот.
Решение:
1. Вариационный ряд
 |
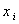-21 | -19 | -18 | -17 | -15 | -13 | -12 | -11 | -9 | -8 | -7 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 |
 |
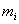2 | 1 | 1 | 1 | 2 | 2 | 3 | 1 | 3 | 5 | 1 | 6 | 5 | 5 | 2 | 3 | 1 | 6 | 5 |
| |
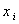3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 28 |
| |
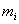2 | 1 | 1 | 1 | 2 | 2 | 3 | 1 | 3 | 5 | 1 | 6 | 5 | 5 | 2 | 3 | 1 | 6 | 5 |
5.1.2. Статистический закон распределения
Длина частичного интервала h рассчитана по формуле
| Интервалы | Относительные частоты |
| [-24,3; -17,7) | 0,04 |
| [-17,7; -11,1) | 0,08 |
| [-11,1; -4,5) | 0,16 |
| [-4,5; 2,1) | 0,27 |
| [2,1; 8,7) | 0,19 |
| [8,7; 5,3) | 0,18 |
| [15,3; 21,9) | 0,07 |
| [21,9; 8,5) | 0,01 |
Несмещенные оценки математического ожидания и дисперсии случайной величины X.
Выборочная средняя находиться по формуле:
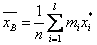, за значение случайной величины будем принимать середину интервала.
 |
|
 |
 |
 |
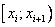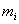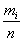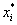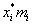| [-24,3; -17,7) | 4 | 0,04 | -21 | -84 |
| [-17,7; -11,1) | 8 | 0,08 | -14,4 | -115 |
| [-11,1; -4,5) | 16 | 0,16 | -7,8 | -125 |
| [-4,5; 2,1) | 27 | 0,27 | -1,2 | -32,4 |
| [2,1; 8,7) | 19 | 0,19 | 5,4 | 102,6 |
| [8,7; 5,3) | 18 | 0,18 | 12 | 216 |
| [15,3; 21,9) | 7 | 0,07 | 18,6 | 130,2 |
| [21,9; 8,5) | 1 | 0,01 | 25,2 | 25,2 |
| Сумма | 117,6 |
| |
|
|
|
|
 |
 |
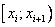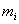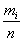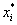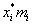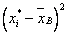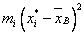| [-24,3; -17,7) | 4 | 0,04 | -21 | -84 | 491,8 | 1967 |
| [-17,7; -11,1) | 8 | 0,08 | -14,4 | -115 | 242,6 | 1941 |
| [-11,1; -4,5) | 16 | 0,16 | -7,8 | -125 | 80,57 | 1289 |
| [-4,5; 2,1) | 27 | 0,27 | -1,2 | -32,4 | 5,645 | 152,4 |
| [2,1; 8,7) | 19 | 0,19 | 5,4 | 102,6 | 17,84 | 339 |
| [8,7; 5,3) | 18 | 0,18 | 12 | 216 | 117,2 | 2109 |
| [15,3; 21,9) | 7 | 0,07 | 18,6 | 130,2 | 303,6 | 2125 |
| [21,9; 8,5) | 1 | 0,01 | 25,2 | 25,2 | 577,2 | 577,2 |
| Сумма | 117,6 | 10500 |
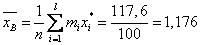
Несмещенной оценкой дисперсии случайной величины является исправленная выборочная дисперсия
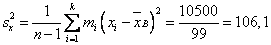
исправленное выборочное среднее квадратическое отклонение случайной величины
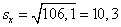
Проверка гипотезы о нормальном законе распределения случайной величины.
С помощью критерия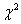 
проверим гипотезу о том, что случайная величина X
имеет нормальный закон распределения с параметрами:
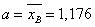
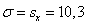
при уровне значимости .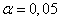
Разобьем ось x на конечное число интервалов так, чтобы в каждый интервал попало не менее 5 наблюденных значений случайной величины X. Тогда, используя статистический закон распределения и объединяя два первых и два последних интервала, получаем:
 |
|
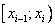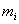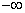[  ;-11,1) |
12 |
| [-11,1; 4,5) | 16 |
| [-4,5; 2,1) | 27 |
| [2,1; 8,7) | 19 |
| [8,7; 15,3) | 18 |
[15,3;  ) |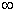
8 |
Вычисляем вероятности попадания случайной величины X, распределенной по нормальному закону с параметрами
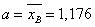
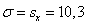
в частичный интервал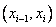 
по формуле
ЭВМ вычисляет значения (в пакете Exel)
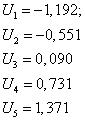
И ЭВМ выдает запрашиваемые значения функции Лапласа
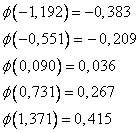
И вычисляем вероятности
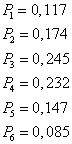
Приведем расчетные таблицы:
 |
 |
 |
 |
 |
 |
|
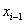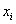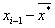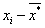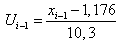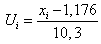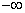-11,1 | — | -12,276 | |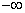
-1,192 |
| -11,1 | -4,5 | -12,276 | -5,676 | -1,192 | -0,551 |
| -4,5 | 2,1 | -5,676 | 0,924 | -0,551 | 0,090 |
| 2,1 | 8,7 | 0,924 | 7,524 | 0,090 | 0,731 |
| 8,7 | 15,3 | 7,524 | 14,124 | 0,731 | 1,371 |
| 15,3 |  |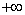
14,124 | — | 1,371 | |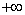
 |
 |
 |
 |
 |
 |
|
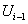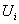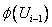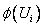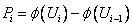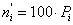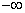-1,192 | -0,5000 | -0,3834 | 0,1166 | 11,66 |
| -1,192 | -0,551 | -0,3834 | -0,2092 | 0,1741 | 17,41 |
| -0,551 | 0,090 | -0,2092 | 0,0357 | 0,2450 | 24,50 |
| 0,090 | 0,731 | 0,0357 | 0,2675 | 0,2317 | 23,17 |
| 0,731 | 1,371 | 0,2675 | 0,4149 | 0,1474 | 14,74 |
| 1,371 | |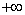
0,4149 | 0,5000 | 0,0851 | 8,51 |
 |
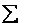1 | 100 |
 |
 |
 |
 |
 |
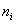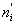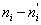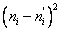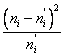| 12 | 11,66 | 0,34 | 0,11 | 0,010 |
| 16 | 17,41 | -1,41 | 2,00 | 0,115 |
| 27 | 24,50 | 2,50 | 6,26 | 0,256 |
| 19 | 23,17 | -4,17 | 17,42 | 0,752 |
| 18 | 14,74 | 3,26 | 10,63 | 0,721 |
| 8 | 8,51 | -0,51 | 0,26 | 0,031 |
| 100 |  |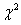
1,885 |
по таблице критических точек распределения 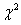, по уровню значимости α = 0,05 и числу степеней свободы k=s—3 = 6—3 = 3 (s—число интервалов) находим критическую точку правосторонней критической области
.
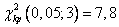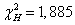
Так как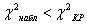 
— гипотеза о нормальном распределении с параметрам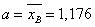и
и 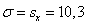принимается.
Кривая распределения нормального закона распределения с
параметрам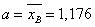и и 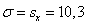построена на одном чертеже с гистограммой относительных частот.
