Задание 2. Пусть над системой двух случайных величин 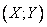 при
при
одинаковых условиях производится 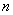 независимых испытаний, и результаты этих испытаний написаны в виде корреляционной таблицы.
независимых испытаний, и результаты этих испытаний написаны в виде корреляционной таблицы.
Требуется:
1) вычислить условные средние случайной величины Y;
2) найти выборочный коэффициент корреляции;
3) найти выборочное корреляционное отношение Y к X ;
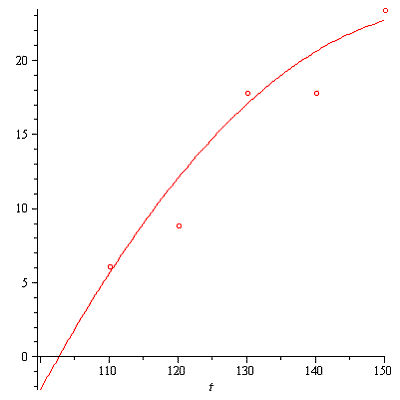
4) в прямоугольной системе координат построить точки 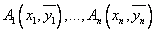
5) записать сумму квадратов отклонений точек,
6) записать систему уравнений для определения неизвестных параметров уравнения регрессии Y на X;
7) найти выборочное уравнение регрессии Y на X ;
8) в прямоугольной системе координат построить кривую регрессии Y на X.
| 2 | 7 | 12 | 17 | 22 | 27 | ||
| 110 | 1 | 5 | 0 | 0 | 0 | 0 | 6 |
| 120 | 0 | 5 | 3 | 0 | 0 | 0 | 8 |
| 130 | 0 | 0 | 3 | 40 | 12 | 0 | 55 |
| 140 | 0 | 0 | 2 | 10 | 5 | 0 | 17 |
| 150 | 0 | 0 | 0 | 3 | 4 | 7 | 14 |
| 1 | 10 | 8 | 53 | 21 | 7 | 100 |
Вычисляем условные средние случайные величины
Необходимо:
а) вычислить групповые средние 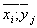 и построить эмпирические линии регрессии;
и построить эмпирические линии регрессии;
Находим групповые средние по формулам:
 , где nij-частоты пар (xi,yj) и ni=
, где nij-частоты пар (xi,yj) и ni=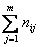 -число интервалов по переменной У.
-число интервалов по переменной У.
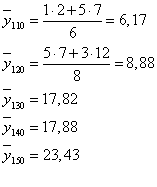
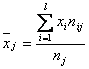 , где nj -число интервалов по переменной Х.
, где nj -число интервалов по переменной Х.
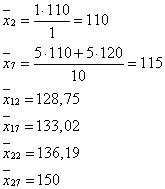
б) По данным таблицы найдем уравнения регрессии У по Х и Х по У:
Находим выборочные характеристики и параметры уравнений регрессии:

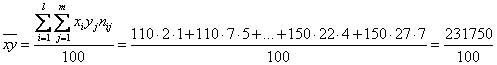
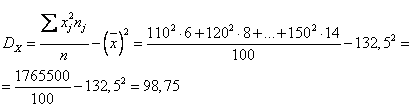
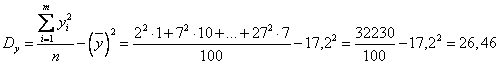
Находим коэффициент корреляции
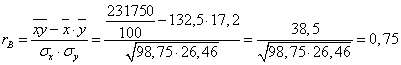 ,
,
Связь между рассматриваемыми переменными прямая и достаточно тесная, он близок к единице.
Выборочное корреляционное отношение Y к X

В прямоугольной системе координат строим точки :
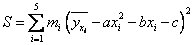 , составим систему
, составим систему

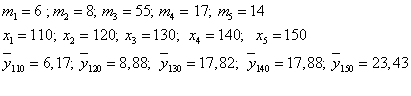
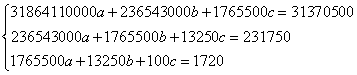
Решаем полученную систему и находим
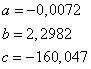
Выборочное уравнение регрессии Y на X имеет вид:
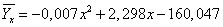
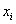 |
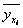 |
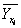 |
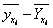 |
| 110 | 6,17 | 5,53 | 0,63 |
| 120 | 8,88 | 11,94 | -3,06 |
| 130 | 17,82 | 16,90 | 0,92 |
| 140 | 17,88 | 20,42 | -2,53 |
| 150 | 23,43 | 22,49 | 0,94 |