По данным, приведенным в таблице:
1) Построить линейное уравнение парной регрессии y на x;
2) Рассчитать линейный коэффициент парной корреляции и оценить тесноту связи;
3) Оценить статистическую значимость параметров регрессии и корелляции, используя F-статистику, t-статистику Стьюдента и путем расчета доверительных интервалов каждого из показателей;
4) Вычислить прогнозное значение y при прогнозном значении x, составляющем 108% от среднего уровня;
5) Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал;
6) Полученные результаты изобразить графически и провести экономическое обоснование.

По территории Центрального района известны данные за 1995 год.

Район	Доля денежных доходов, направленных на покупку валюты, в общей сумме среднедушевого денежного дохода, % у	Среднемесячная начисленная заработная плата, тыс. руб. х
Брянская обл.	6,9	289
Владимирская обл.	8,7	334
Ивановская обл.	6,4	300
Калужская обл.	8,4	343
Костромская обл.	6,1	356
Орловская обл.	9,4	289
Рязанская обл.	11	341
Смоленская обл.	6,4	327
Тверская обл.	9,3	357
Тульская обл.	8,2	352
Ярославская обл.	8,6	381

Решение.

1. Заполним таблицу экспериментальных данных, за исключением двух последних столбцов.

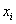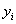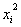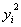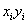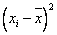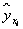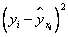1	289	6,9	83521	47,61	1994,1	1984,298	7,64216	0,550802
2	334	8,7	111556	75,69	2905,8	0,206612	8,132223	0,322371
3	300	6,4	90000	40,96	1920	1125,298	7,761953	1,854917
4	343	8,4	117649	70,56	2881,2	89,38843	8,230235	0,02882
5	356	6,1	126736	37,21	2171,6	504,2066	8,371809	5,161116
6	289	9,4	83521	88,36	2716,6	1984,298	7,64216	3,090001
7	341	11	116281	121	3751	55,57025	8,208455	7,792724
8	327	6,4	106929	40,96	2092,8	42,84298	8,055991	2,742306
9	357	9,3	127449	86,49	3320,1	550,1157	8,382699	0,84144
10	352	8,2	123904	67,24	2886,4	340,5702	8,328248	0,016448
11	381	8,6	145161	73,96	3276,6	2251,934	8,644066	0,001942
Сумма:	3669	89,4	1232707	750,04	29916,2	8928,727	89,4	22,40289

Найдем параметры линейной регрессии

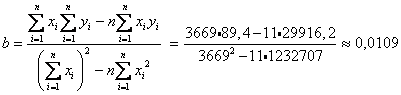
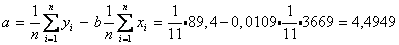
Следовательно, уравнение регрессии имеет вид

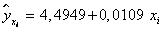
Значит, при увеличении среднемесячной начисленной заработной платы на 1 тысячу рублей доля денежных доходов, направленных на покупку валюты, в общей сумме среднедушевого денежного дохода увеличивается в среднем на 0,0109%.

С помощью найденного уравнения регрессии заполняем два последних столбика таблицы, учитывая, что среднее значение независимой переменной

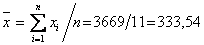
2. Рассчитаем линейный коэффициент парной корреляции

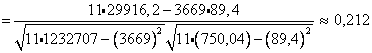
Связь очень хорошая.

3. Используя данные из таблицы, найдем интервальные оценки параметров регрессии с 95% надежностью.
Стандартная ошибка оценки равна

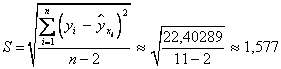
Интервал для свободного члена регрессии (параметра А)


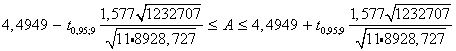
Коэффициент Стьюдента 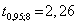, следовательно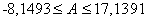

Интервальная оценка для коэффициента регрессии 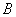определяется по следующей формуле

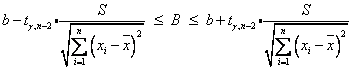
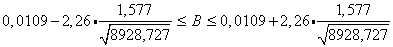
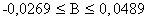
Т.е. с надежностью 0,95 при увеличении зарплаты на 1 тысячу затраты увеличатся на величину, заключенную в пределах от -0,0269 до 0,0489 %.

Оценим значимость коэффициентов регрессии и корелляции с помощью t-статистики Стьюдента. Для этого необходимо сравнить табличное значение t-критерия (для уровня значимость 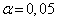и числа степеней свободы 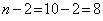) с расчетными критериями :

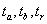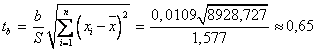
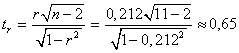
Коэффициент Стьюдента 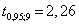, следовательно, фактические значения не превосходят табличное значение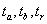

; ;

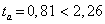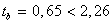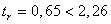
И коэффициенты 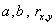не значимы.

4) Вычислим прогнозное значение y при прогнозном значении x, составляющем 108% от среднего уровня.

,

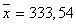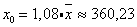
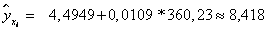
5) Оценим точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.

Индивидуальные значения урожайности 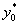принадлежат промежутку

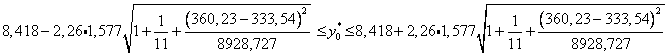
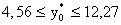
6) Нанесем экспериментальные точки на координатную плоскость, построим уравнение регрессии (точки – наблюдаемые значения, прямая – линия регрессии)

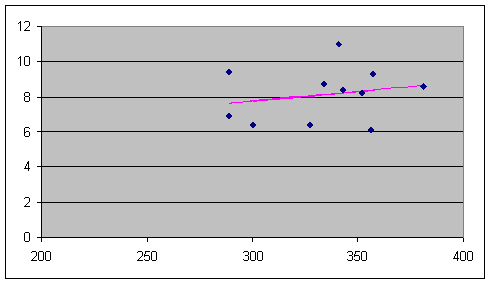
Нельзя сделать вывод о правомочности применения линейной регрессионной модели.