Используя данные, приведенные в таблице:
1) Построить линейное уравнение множественной регрессии;
2) Оценить значимость параметров данного уравнения построить доверительные интервалы для каждого из параметров, оценить значимость уравнения в целом, пояснить экономический смысл полученных результатов;
3) Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной детерминации, сравнить их с линейными коэффициентами парной корреляции, пояснить различия между ними;
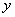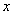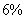4) Вычислить прогнозное значение при уменьшении вектора на от максимального уровня, оценить ошибку прогноза и построить доверительный интервал прогноза

Номер наблюдения, i	y	x1	x2
1	1,4	9,8	12,6
2	0,4	19,5	12,2
3	0,8	6,8	3,2
4	1,8	27,0	13,0
5	0,9	12,4	6,9
6	1,1	17,7	15,0
7	1,9	12,7	11,9
8	0,9	21,4	1,6
9	1,3	13,5	8,6
10	2,0	13,4	11,5
11	0,4	2,0	1,4
12	0,6	4,2	1,9

1) Предполагается, что объясняемая переменная 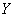зависит от двух факторов 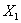и 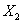, поэтому уравнение регрессии будем искать в виде

,
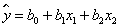где 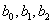— параметры модели. Переходя к матричному описанию задачи, обозначим
, ,
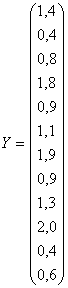при этом необходимо найти матрицу параметров модели

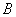
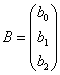
по формуле .

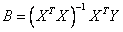Найдем матрицу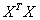

Найдем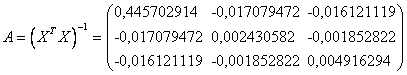

Найдем произведение матриц

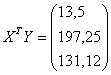
Найдем матрицу параметров модели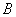

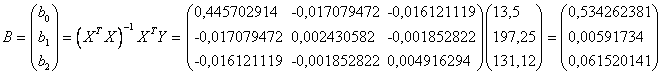
Таким образом, уравнение регрессии имеет вид

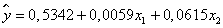
2) Оценим значимость параметров данного уравнения и построим доверительные интервалы для каждого из параметров, оценим значимость уравнения в целом, поясним экономический смысл полученных результатов.

Используя начальные данные и полученное уравнение, заполним следующую таблицу:

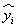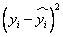1	1,4	1,367406	0,001062
2	0,4	1,400196	1,000393
3	0,8	0,771365	0,00082
4	1,8	1,493792	0,093763
5	0,9	1,032126	0,017457
6	1,1	1,561801	0,213261
7	1,9	1,341502	0,31192
8	0,9	0,759326	0,019789
9	1,3	1,14322	0,02458
10	2,0	1,321036	0,460992
11	0,4	0,632225	0,053929
12	0,6	0,676003	0,005777
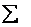	13,5	13,5	2,203742

Остаточная дисперсия определяется выражением

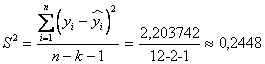
а дисперсии параметров уравнения регрессии равны


.

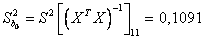
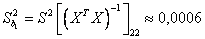
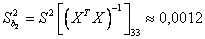Доверительный интервал для параметра 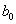найдем по формуле

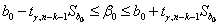
Коэффициент Стьюдента 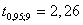, следовательно

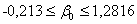
Аналогично получим

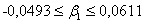
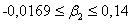
Для оценки значимости параметров уравнения регрессии сравним 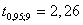с наблюдаемыми критериями

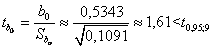
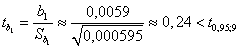
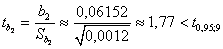
Анализ показывает, что при надежности 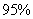все коэффициенты незначимы.

Оценим общее качество уравнения регрессии. Используя начальные данные и полученное уравнение, заполним следующую таблицу:

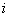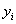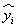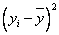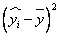1	1,4	1,367406	0,075625	0,058761
2	0,4	1,400196	0,525625	0,075733
3	0,8	0,771365	0,105625	0,125058
4	1,8	1,493792	0,455625	0,136008
5	0,9	1,032126	0,050625	0,008626
6	1,1	1,561801	0,000625	0,190795
7	1,9	1,341502	0,600625	0,046873
8	0,9	0,759326	0,050625	0,133717
9	1,3	1,14322	0,030625	0,000332
10	2,0	1,321036	0,765625	0,03843
11	0,4	0,632225	0,525625	0,242827
12	0,6	0,676003	0,275625	0,201598
Сумма	13,5	13,5	3,4625	1,258758

Найдем индекс корреляции

,
при этом скорректированный коэффициент детерминации равен

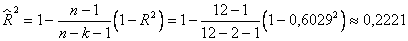
Проверим значимость уравнения регрессии, при этом должно выполняться неравенство

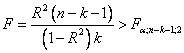
Наблюдаемый критерий равен

,
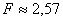а 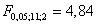, следовательно, уравнение регрессии незначимо при .

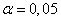3) Рассчитаем линейные коэффициенты частной корреляции и сравним их с линейными коэффициентами парной корреляции

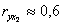
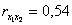
Рассмотрев межфакторный коэффициент корреляции 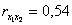можно сказать, что явная линейная связь между факторам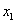и и 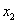слабая и возможно введение их как двух отдельных факторов в модель. Парные коэффициенты 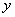с каждым из факторов 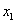и 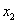показывают наличие положительной линейной связи, при связь с первым фактором очень слабая, а со вторым — сильнее.

Частные коэффициенты корреляции найдем по формулам

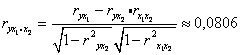
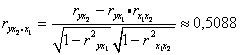
Их значения показывают, что при отсутствии влияния других факторов, связь с рассматриваемым фактором увеличивается.

4. Рассчитаем прогнозное значение результата, если прогнозные значения факторов составляют 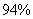от их максимального значения.

Для этого в полученное равнение регрессии подставим ; :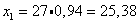

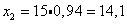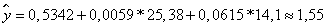
Доверительный интервал найдем по формуле

,
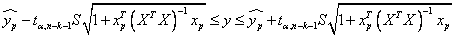где

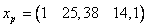
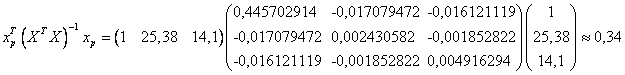
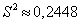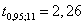, , т.о. 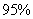доверительный интервал прогноза имеет вид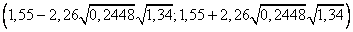

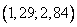
Построенная линейная модель выявила положительную зависимость объясняемой переменной Y от объясняющих факторов.