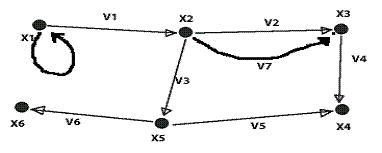
Дано

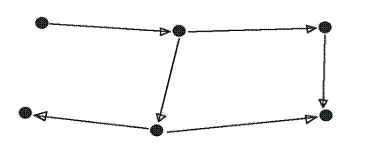
Обозначим вершины и ребра

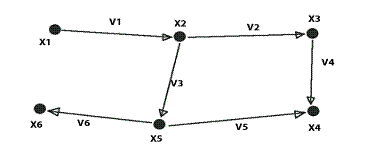
Задание 1.
Задать граф следующими способами: перечислением, матрицами смежности и инцидентности.
Решение:
Перечисление:
Множество вершин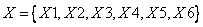
Множество связей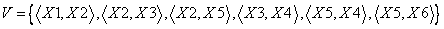
Множество изолированных вершин пусто.
Матрица инцидентности

	V1	V2	V3	V4	V5	V6
X1	1	0	0	0	0	0
X2	-1	1	1	0	0	0
X3	0	-1	0	1	0	0
X4	0	0	0	-1	-1	0
X5	0	0	-1	0	1	1
X6	0	0	0	0	0	-1

Матрица смежности

	X1	X2	X3	X4	X5	X6
X1	0	1	0	0	0	0
X2	0	0	1	0	1	0
X3	0	0	0	1	0	0
X4	0	0	0	0	0	0
X5	0	0	0	1	0	1
X6	0	0	0	0	0	0

Задание 2.
Определить следующие основные характеристики графа:
— число ребер и дуг,
— число вершин,
— коэффициент связности графа,
-степени всех вершин,
-цикломатическое число графа.

Решение:
Число ребер – 0, дуг – 6.
Число вершин – 6.
Коэффициент связности графа- 1
Степени всех вершин

	X1	X2	X3	X4	X5	X6
Полустепень исхода	1	2	1	0	2	0
Полустепень захода	0	1	1	2	1	1
Степень	1	3	2	2	3	1

Цикломатическое число графа = (число связей – число вершин)+ коэффициент связности. Т.е. 6-6+1=1

Задание 3.
Определить, является ли данный граф:
— планарным или плоским графом (обосновать ответ и выполнить обратное преобразование);
— двудольным графом ( обосновать ответ и, если необходимо, то достроить до двудольного графа);
— деревом ( обосновать ответ и, в случае циклического графа, привести один из вариантов основного дерева)
— псевдографом или мультиграфом, или простым графом ( обосновать ответ и выполнить необходимые преобразования)
Решение:
Данный граф является плоским, поскольку все его связи пересекаются только в вершинах. Преобразуем данный граф в планарный.

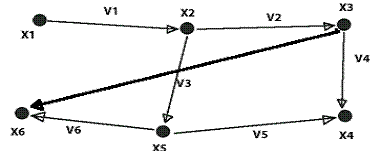
Данный граф является двудольным:

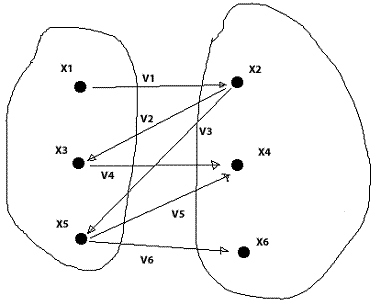
Данный граф не является деревом, поскольку он содержит циклы. Приведем пример остова данного графа.

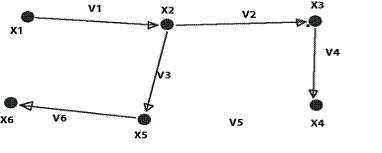
V1,V2,V3,V4,V6 – ветви, V5 — хорда.
Данный граф является простым, поскольку не содержит петли, изолированные вершины и кратные связи.
Преобразуем данный граф в мультиграф:

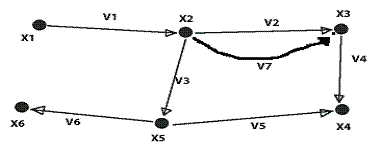
Преобразуем исходный граф в псевдограф:

Задание 4.
Привести пример подграфа, частичного графа и частичного подграфа.
Решение:
Подграф

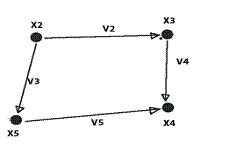
Частичный подграф

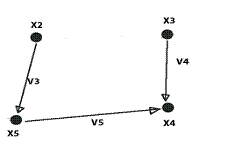
Частичный граф

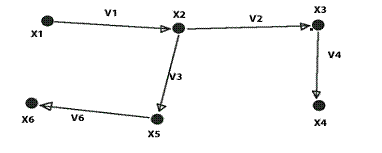
Задание 5.
Провести реберную и вершинную раскраски графа с определением вершинного и реберного хроматического числа.
Обозначим цвета числами натурального ряда, номер рядом с каждой вершиной или связью будет обозначать цвет.
Решение:
Вершинная раскраска:

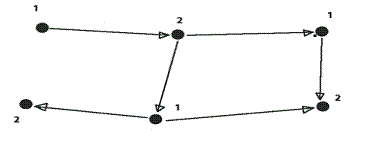
Вершинное хроматическое число равно 2.
Реберная раскраска

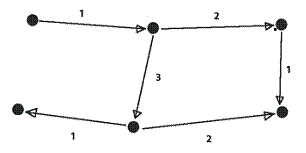
Реберное хроматическое число равно 3.