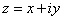Для следующих задач используется условия Коши-Римана ( они же условия Даламбера — Эйлера)
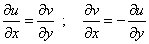
1.
Восстановить голоморфную функцию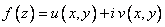 
по заданной действительной части 
.
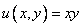Так как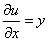 
, 
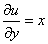, то, из условий Коши-Римана,
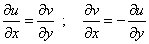
находим производные
.
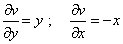Из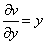 
получим
.
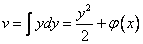Для определения функции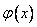 
дифференцируем выражение 
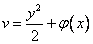по 
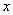и подставим в 
.
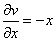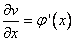
Подставим:
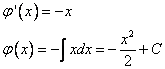
Значит :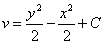 
.
Окончательно получаем
Ответ:
, где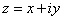 
14. Восстановить голоморфную функцию 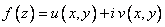по заданной действительной части 
.
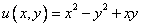Так как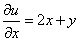 
, 
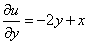, то, из условий Коши-Римана
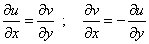
находим производные
.
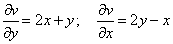Из
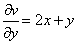получим
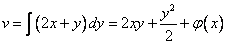.Для определения функции
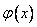дифференцируем выражение 
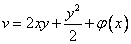по 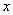и подставим в 
.
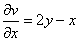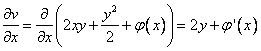
Подставим:
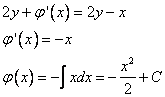
Значит :
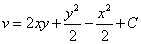.Окончательно получаем
Ответ:
, где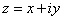
3. Восстановить голоморфную функцию 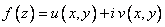по заданной мнимой части 
.
Так как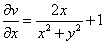 
, 
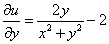, то, из условий Коши-Римана
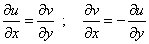
находим производные
.
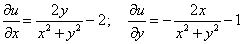Из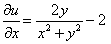 
получим
.
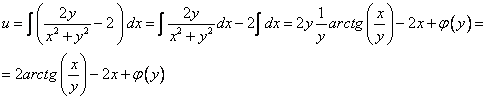Для определения функции 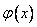дифференцируем выражение 
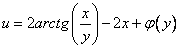по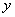 
и подставим в .
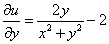Подставим:
Значит :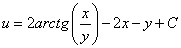 
.
Окончательно получаем
Ответ:
, где