1. В аналитическом отделе фирмы 8 менеджеров и 12 финансистов. Для выполнения задания случайным образом из списка выбирают 3 человек. Найти вероятность того, что менеджеров среди них будет:
а) ровно два;
б) не менее одного.
Решение:
Задача решается по классическому определению вероятности :
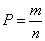, где n – количество всевозможных исходов эксперимента, m – количество исходов, благоприятствующих появлению рассматриваемого события.
А) Обозначим событие А – среди выбранных 3-х человек будет ровно 2 менеджера.
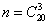— количество способов выбора из всех 20 человек трех произвольных.
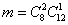— количество способов, которыми можно из всех 8-ми менеджеров выбрать двух и из 12 финансистов выбрать оставшегося третьего человека.

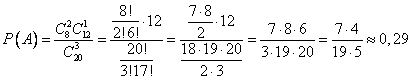
Б) Обозначим событие B – среди выбранных 3-х человек будет не менее одного менеджера, то есть либо один, либо два, либо все три. По теореме сложения вероятностей:

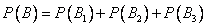
Аналогично предыдущему случаю:

Ответ: а) 0,29, б) 0,81

2. Вероятность того, что в страховую компанию в течение года обратится с иском о возмещении ущерба первый клиент, равна 0,18. Для второго клиента вероятность такого обращения равна 0,23 Для третьего клиента – 0,13. Найти вероятность того, что в течение года в страховую компанию обратится хотя бы один клиент, если обращения клиентов — события независимые.
Решение:
Обозначим события:
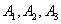— первый, второй или третий клиент обращаются с иском.
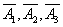— первый, второй или третий клиент не обращаются с иском.
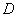— хотя бы один клиент обратился с иском.
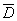— противоположное событие, т.е., что ни один клиент не обратился с иском.
Задача решается по формуле вероятности обратного события.
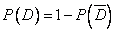. Используем формулы умножения вероятностей.


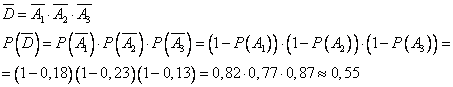
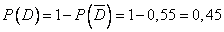
Ответ: 0,45

3. В консультационной фирме 24% сотрудников получает высокую заработную плату. Известно также, что женщины составляют 43% сотрудников фирмы, при этом 6,7% сотрудников – женщины, получающие высокую заработную плату. Можно ли утверждать, что в консультационной фирме существует дискриминация женщин в оплате труда? Ответ объяснить, сформулировав решение задачи в терминах теории вероятностей.
Решение:
Обозначим события
А- сотрудник получает высокую зарплату.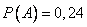
В- сотрудник является женщиной.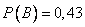
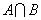— женщина получает высокую зарплату,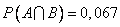
Проверим, являются ли события А и В независимыми, т.е. верно ли равенство

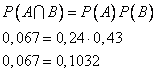
Равенство неверное, т.е. события «сотрудник — женщина» и «сотрудник получает высокую зарплату» зависимы.
Ответ: Дискриминация по половому признаку существует.

4. В брокерской компании, в которой 33% составляют сотрудники первого отдела, 28% — второго, остальные третьего, результаты работы оцениваются по отдаче с каждого инвестированного сотрудником рубля (высокая или низкая). Анализ последнего месяца работы показал, что низкую отдачу имеют 2,3% сотрудников первого отдела, 1,3% — второго и 1,8% — третьего отдела. Какова вероятность того, что случайно выбранный сотрудник компании за последний месяц показал высокую отдачу? Если сотрудник показал низкую отдачу, то в каком отделе, скорее всего, он работает?
Решение:
Обозначим события:
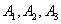— сотрудник из первого, второго или третьего отдела.

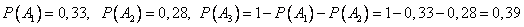
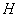— сотрудник показал высокую отдачу.
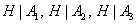— низкая отдача сотрудника, при условии, что он из соответствующего отдела

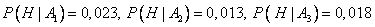
Используем формулу полной вероятности.

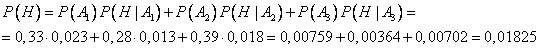
Вероятность обратного события, т.е. высокой отдачи сотрудника:

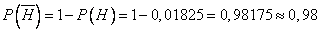
Ответим на второй вопрос задачи:
Если сотрудник показал низкую отдачу, то в каком отделе, скорее всего, он работает?
Используем формулу Байеса и найдем вероятности того, что сотрудник работает в соответсвующем отделе, при условии, что он показал низкую отдачу.

Вывод: сотрудник, вероятнее всего, работает в первом отделе.

5. В рамках маркетингового исследования нового товара компания-производитель проверяет спрос на него по результатам отзывов случайно выбранных потенциальных покупателей. Для определенного товара известно, что вероятность его возможного успеха на рынке составит 0,78, если товар действительно удачный, и 0,18 если он неудачен. Из прошлого опыта известно, что новый товар может иметь успех на рынке с вероятностью 0,60. Если новый товар прошел выборочную проверку, и ее результаты указали на возможный его успех, то чему равна вероятность того, что это действительно так?
Решение:
Задача решается по формуле Байеса. Обозначим события.
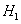— товар удачен.
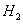— товар не удачен.
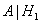— товар успешен на рынке при условии, что сам он удачен.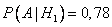
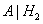— товар успешен на рынке при условии, что сам он неудачен.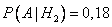
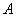— товар успешен на рынке. .
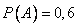Составим формулу полной вероятности, учитывая, что гипотезы 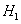и 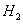представляют собой полную группу событий.

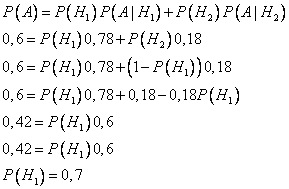
Известно, что событие А состоялось, т.е. товар получил успех на рынке. Чему равно ?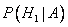
Составим формулу Байеса

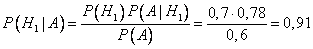
Ответ: 0,91