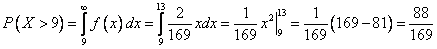6. Отдел менеджмента одного из предприятий разрабатывает новую стратегию выпуска продукции. Известно, что при определенном технологическом процессе 78% всей продукции предприятия — высшего сорта, а всего производится 230 изделий. Стратегия, разработанная отделом менеджмента, основана на том, что предприятие будет рентабельным, если выпуск продукции высшего сорта будет составлять не менее 180 изделий. Оценить критически новую стратегию выпуска продукции (определив наивероятнейшее число изделий высшего сорта из 230 изделий и вероятность этого события).
Решение: Наивероятнейшее число 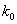 определяется из двойного неравенства
определяется из двойного неравенства
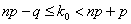
Подставим 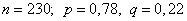
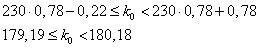
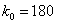
Найдем вероятность наивероятнейшего числа изделий высшего сорта по локальной теореме Лапласа
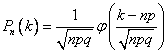
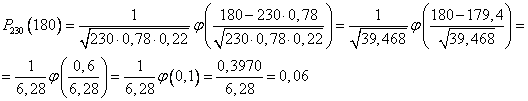
Ответ: Наивероятнейшее 180 шт, вероятность этого 0,06
7. Торговый агент в среднем контактирует с 4 потенциальными покупателями в день. Из опыта ему известно, что вероятность того, что потенциальный покупатель совершит покупку, равна 0,33. Составить закон распределения ежедневного числа продаж для агента. Найти числовые характеристики этого распределения. Чему равна вероятность того, что у агента будет хотя бы 2 продажи в течение дня?
Решение:
Пусть Х – количество ежедневных продаж. Оно может принимать значения 0,1,2,3,4. Найдем вероятности появления соответствующих значений, используя для вычисления формулу Бернулли.
1) пусть Х=0. Найдем вероятность того, что торговый агент не сделал ни одной продажи.
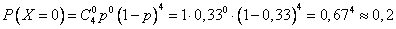
2) Х=1, т.е. одна продажа есть.
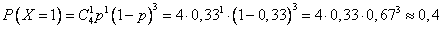
3) Х=2, т.е. произошло две продажи.
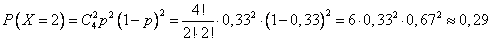
4) Х=3, т.е. произошло три продажи.
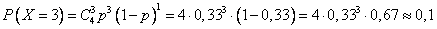
5) Х=4, т.е. произошло четрые продажи.
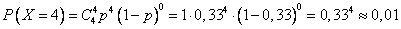
Проверка: 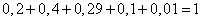
Составим закон распределения:
| Х | 0 | 1 | 2 | 3 | 4 |
| Р | 0,2 | 0,4 | 0,29 | 0,1 | 0,01 |
Найдем математическое ожидание
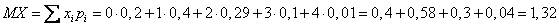
Найдем дисперсию:
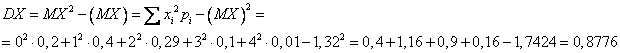
Найдем среднеквадратическое отклонение:
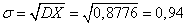 .
.
Найдем вероятность того, что за день было хотя бы две продажи, т.е. 2,3 или 4.
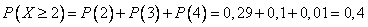
8. Дискретная случайная величина Х с математическим ожиданием М(Х)=5,2 задана рядом распределения
| xi | -9 | 0 | 7 | 20 |
| pi | p1 | 0,4 | p3 | 0,2 |
а) Найти р1 и р3;
б) построить многоугольник распределения;
в) построить интегральную функцию распределения F(x) и ее график;
г) вычислить дисперсию D(X); пояснить, как можно интерпретировать ее значение.
Решение:
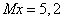
Две неизвестные в законе распределения, значит, нужны два уравнения:
1) 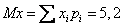
2) 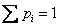
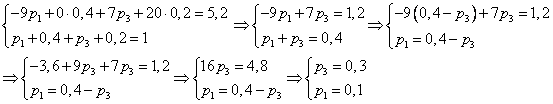
Итого, закон распределения имеет вид
| xi | -9 | 0 | 7 | 20 |
| 0,1 | p1 | 0,4 | 0,3 | 0,2 |
Б) построить многоугольник распределения;
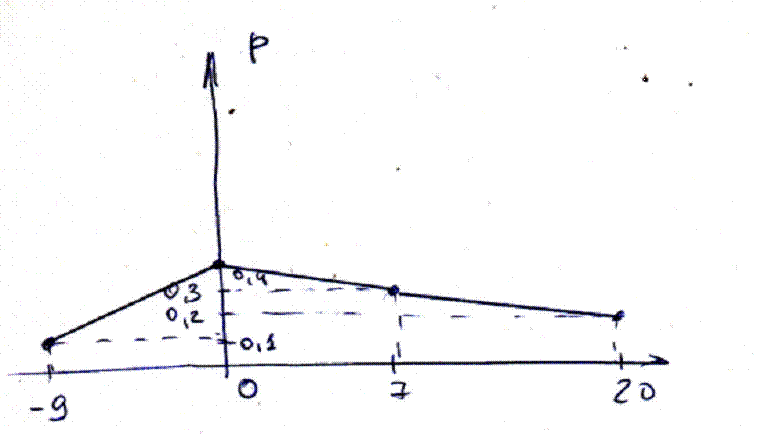
В) построить интегральную функцию распределения F(x) и ее график;
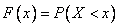
1) 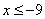
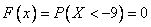
2) 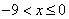
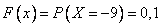
3) 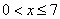
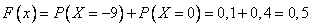
4) 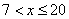
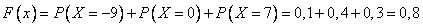
5) 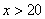
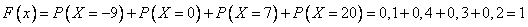
Функция распределения имеет вид:

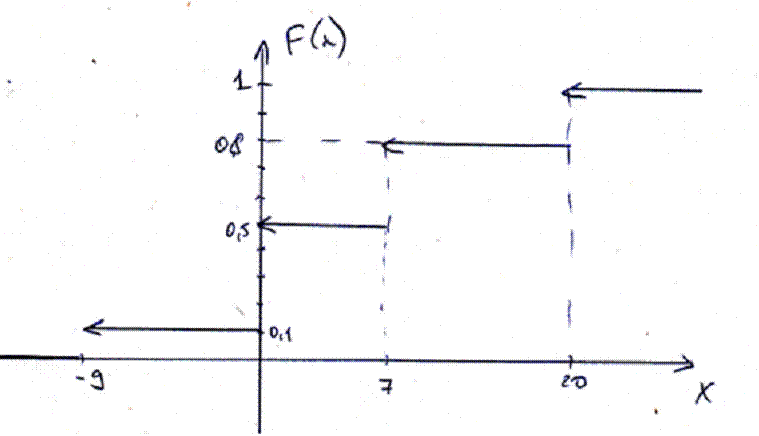
В) вычислить дисперсию D(X); пояснить, как можно интерпретировать ее значение.

9. В нормально распределенной совокупности 18% значений случайной величины X меньше 14 и 48% значений случайной величины X больше 20. Найти параметры этой совокупности.
Решение:
Используем формулу:
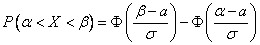
Составим уравнения:
1)
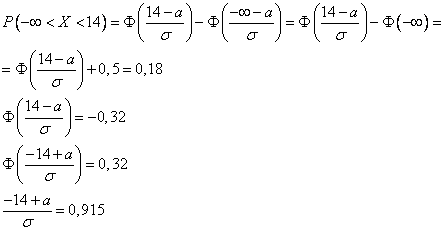
2)
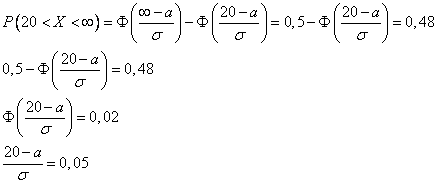
Запишем систему:
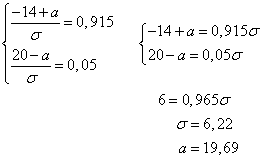
Ответ: 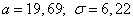
10. Прибыль от реализации инноваций в течение месяца описывается следующей функцией плотности распределения вероятностей
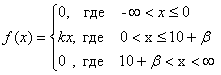 где β=3
где β=3
Найти:
а) параметр k;
б) среднюю ожидаемую прибыль;
в) интегральную функцию распределения F(x) и ее график;
г) вероятность того, что прибыль от реализации инноваций составит больше, чем 9.
Решение:
Плотность распределения имеет вид: 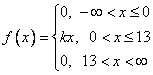
А) параметр k.
Используем свойство плотности распределения
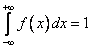 .
.

Итого, плотность имеет вид:
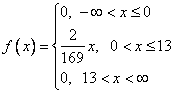
Б) Средняя ожидаемая прибыль.
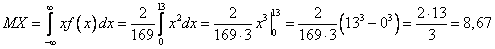
В) Найдем интегральную функцию распределения и ее график.
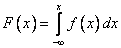
А) 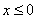 , f(x)=0
, f(x)=0
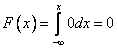
Б) 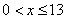 ,
, 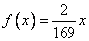
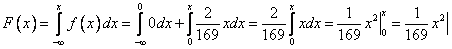
В) 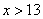 ,
, 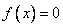
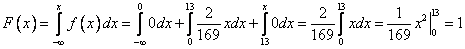
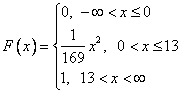
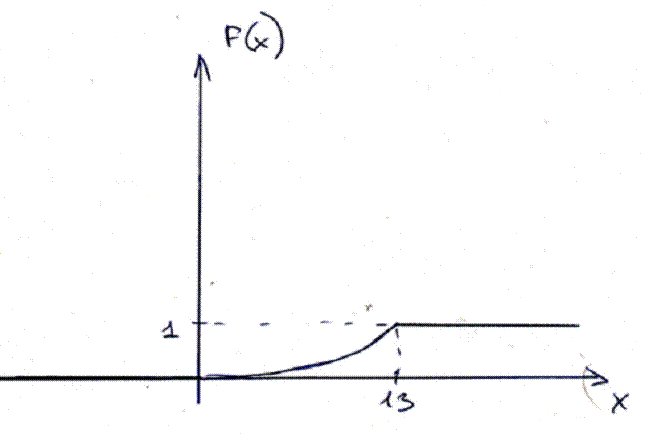
Вычислим вероятность того, что прибыль от реализации инноваций составит больше, чем 9.