11. Случайная величина имеет биноминальное распределение с математическим ожиданием M(X)=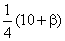 и дисперсией D(X)= 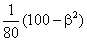, где β=3. Найти Р(X ≥ 2).
Решение:
Общий вид биномиального распределения :
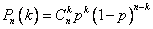, В условии дано, что .
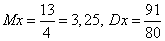Известно, что для этого типа распределения 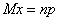, а .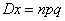
Составим систему уравнений.

Распределение имеет вид: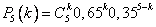

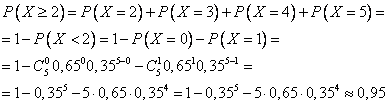
Ответ: 0,95
12. Сумма всех вкладов в некотором банке составляет 5•10⁶ руб., а вероятность того, что случайно выбранный вклад не превышает 4•10⁴ руб., равна 0,8. Каково число вкладчиков данного банка?
Решение:
Используем неравенство Маркова: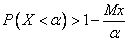
Подставим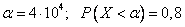

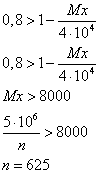
Ответ: 625 вкладчиков.

13. В среднем за час автомойку посещает 5 клиентов. Найти вероятность того, что за два часа автомойку посетят не менее 7 клиентов, и вероятность того, что в течение как минимум 19 минут на автомойке не будет ни одного клиента. Число посетителей за час распределено по закону Пуассона, а время ожидания клиента распределено по показательному закону (см. данные в таблице).
Решение:
1) За два часа не менее 7 клиентов.
Формула Пуассона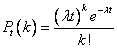

Найдем вероятность того, что автомойку посетят 0,1,2,3,4,5 или 6 клиентов.
Поставим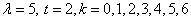

Т.е. вероятность того, что клиентов будет не менее 7 равна:

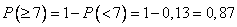
2) вероятность того, что в течение как минимум 19 минут на автомойке не будет ни одного клиента
Время ожидания клиента распределено по показательному закону.

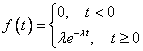
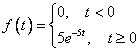
Найдем вероятность того, что время ожидания клиента заключено в интервале от 0 до .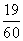

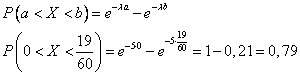
Тогда вероятность того, что время ожидания превысит 19 минут будет равно 0,79.
Ответ: 0,79