15. Администрацию универсама интересует оптимальный уровень запасов продуктов в торговом зале, а также среднемесячный объем продаж товаров, не являющихся предметом ежедневного потребления в семье (таких, например, как сода). Для выяснения этого вопроса менеджер универсама в течение месяца регистрировал продажи соды и представил результаты в виде дискретного вариационного ряда
| xi | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| mi | 2 | 3 | 12 | 5 | 5 | 2 | 1 |
Требуется:
а) построить полигон относительных частот 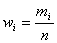 ;
;
Вычислим относительные частоты:
| xi | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| mi | 2 | 3 | 12 | 5 | 5 | 2 | 1 |
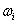 |
0,07 | 0,10 | 0,40 | 0,17 | 0,17 | 0,07 | 0,03 |
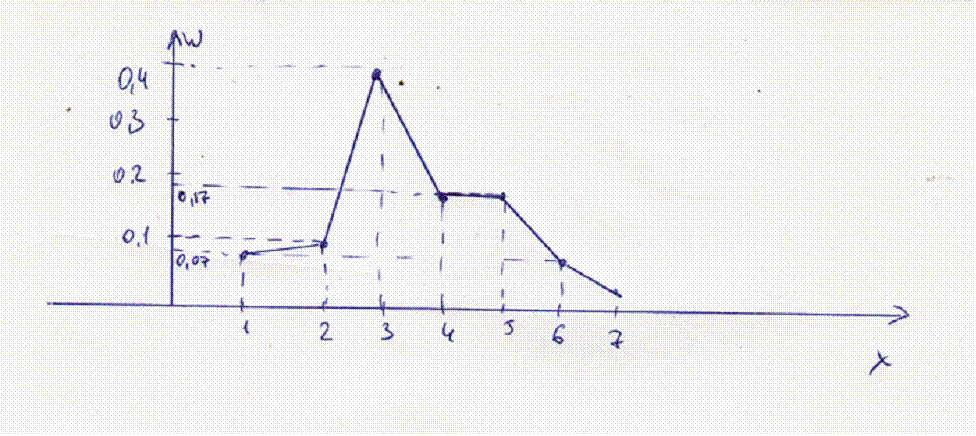
б) вычислить среднее выборочное 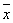 , выборочную дисперсию D(x) и среднее выборочное квадратичное отклонение σ(x).
, выборочную дисперсию D(x) и среднее выборочное квадратичное отклонение σ(x).
Вычислим выборочное среднее по формуле 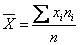
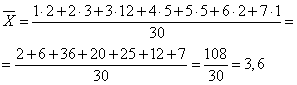
Найдем выборочную дисперсию по формуле:
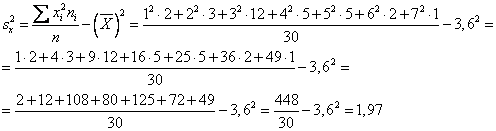
Среднее выборочное квадратичное отклонение σ(x).
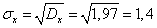
16. При изучении структуры коммерческих банков по объявленному уставному фонду из трех тысяч банков страны было отобрано по схеме собственно случайной бесповторной выборки сто. Данные о распределении банков по этому признаку представлены в таблице:
| Размер уставного фонда | xmin | До 40 | 40 | 80 | 120 | 160 | Свыше 200 | Итого |
| xmax | 80 | 120 | 160 | 200 | ||||
| Число банков | ni | 7 | 9 | 18 | 34 | 22 | 10 | 100 |
Найти:
а) вероятность того, что средний размер уставного фонда всех коммерческих банков отличается от среднего размера его в выборке не более чем на пять миллионов рублей (по абсолютной величине);
Найдем выборочную среднюю и исправленное выборочное среднеквадратичное отклонение. За значение признака на интервале примем его середину.
| Min | Max | 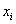 |
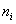 |
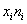 |
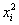 |
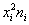 |
| — | 40 | 20 | 7 | 140 | 400 | 2800 |
| 40 | 80 | 60 | 9 | 540 | 3600 | 32400 |
| 80 | 120 | 100 | 18 | 1800 | 10000 | 180000 |
| 120 | 160 | 140 | 34 | 4760 | 19600 | 666400 |
| 160 | 200 | 180 | 22 | 3960 | 32400 | 712800 |
| 200 | — | 220 | 10 | 2200 | 48400 | 484000 |
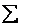 |
100 | 13400 | 2078400 |
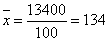
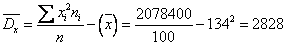
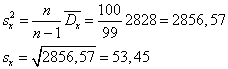
Найдем среднюю квадратическую ошибку выборки для средней для бесповторной выборки
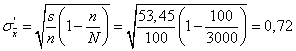
Найдем вероятность по формуле:
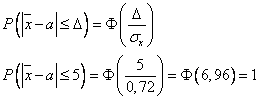
б) границы, в которых с вероятностью 0,9 заключена доля всех банков, размер уставного фонда которых не менее 160 миллионов рублей;
N=3000, n=100, m=32.
Выборочная доля всех банков, размер уставного фонда, который не менее шестидесяти миллионов 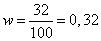
Найдем среднюю квадратичную ошибку бесповторной выборки для доли:
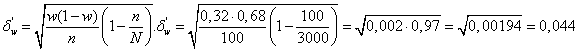
Учитывая, что 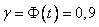 , то t=1,65. Найдем предельную ошибку выборки для доли:
, то t=1,65. Найдем предельную ошибку выборки для доли: 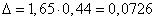 .
.
Теперь искомый доверительный интервал определяем как:
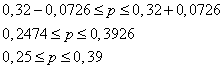
Вывод: С вероятностью 0,9, доля всех банков, размер уставного капитала которых не менее 160 миллионов рублей, заключена от 0,25 до 0,39
в) объем бесповторной выборки, при котором то же отклонение среднего размера уставного фонда всех банков (не более пяти миллионов рублей см. пункт а)), можно гарантировать с вероятностью 0,95.
В качестве неизвестного значения 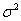 для определения объема выборки берем его состоятельную оценку
для определения объема выборки берем его состоятельную оценку 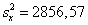 . Учитывая, что
. Учитывая, что 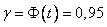 и по таблице t = 1,96.
и по таблице t = 1,96.
Объем бесповторной выборки:
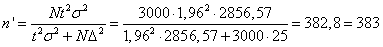
Ответ: объем выборки должен быть 383 единицы.
17. Необходимо:
а) выдвинуть гипотезу о виде модели, аппроксимирующей эмпирическое распределение, обосновав выбор;
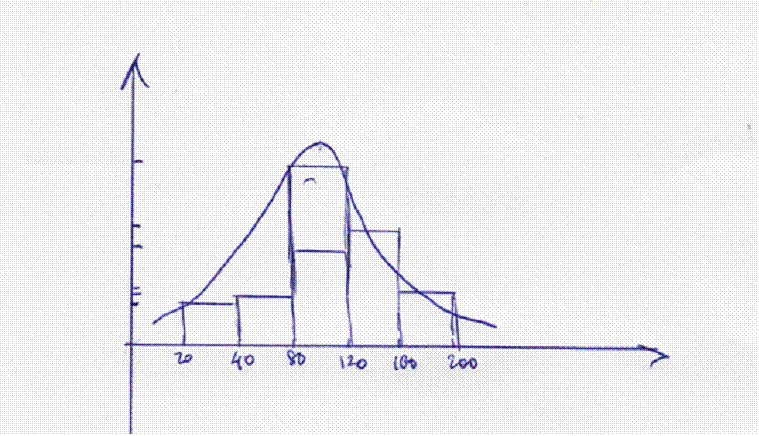
Выдвинем гипотезу о том, что эмпирическое распределение аппроксимирует нормальное распределение. Основание – диаграмма напоминает колокол, т.е. нормальную кривую.
б) используя χ2 — критерий Пирсона, при уровне значимости α=0,05 проверить гипотезу о том, что случайная величина Х – размер уставного фонда распределена по нормальному закону.
Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.
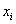 |
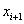 |
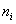 |
|
| 1 | — | 40 | 7 |
| 2 | 40 | 80 | 9 |
| 3 | 80 | 120 | 18 |
| 4 | 120 | 160 | 34 |
| 5 | 160 | 200 | 22 |
| 6 | 200 | — | 10 |
| 100 |
Вычислим выборочную среднюю и выборочное среднее квадратическое отклонение методом произведений. Для этого перейдем от заданного интервального распределения к распределению равноотстоящих вариант, приняв в качестве варианты среднее арифметическое концов интервала: 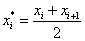
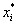 |
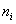 |
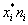 |
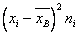 |
| 20 | 7 | 140 | 90972 |
| 60 | 9 | 540 | 49284 |
| 100 | 18 | 1800 | 20808 |
| 140 | 34 | 4760 | 1224 |
| 180 | 22 | 3960 | 46552 |
| 220 | 10 | 2200 | 73960 |
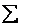 |
13400 | 282800 | |
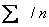 |
134 | 2828 | |
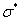 |
53,18 |
2. Найдем интервалы 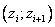 , левый край первого примем равным
, левый край первого примем равным 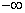 , а правый последнего
, а правый последнего 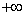 :
:
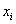 |
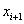 |
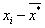 |
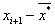 |
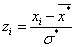 |
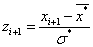 |
| 0 | 40 | — | -94,000 | 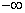 |
-1,768 |
| 40 | 80 | -94,000 | -54,000 | -1,768 | -1,015 |
| 80 | 120 | -54,000 | -14,000 | -1,015 | -0,263 |
| 120 | 160 | -14,000 | 26,000 | -0,263 | 0,489 |
| 160 | 200 | 26,000 | 66,000 | 0,489 | 1,241 |
| 200 | 240 | 66,000 | — | 1,241 | 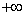 |
3. Найдем теоретические вероятности 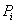 и теоретические частоты
и теоретические частоты 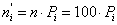 . Для этого составим расчетную таблицу
. Для этого составим расчетную таблицу
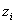 |
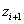 |
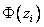 |
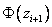 |
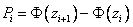 |
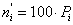 |
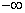 |
-1,768 | -0,500 | -0,461 | 0,039 | 3,856 |
| -1,768 | -1,015 | -0,461 | -0,345 | 0,116 | 11,639 |
| -1,015 | -0,263 | -0,345 | -0,104 | 0,241 | 24,123 |
| -0,263 | 0,489 | -0,104 | 0,188 | 0,291 | 29,137 |
| 0,489 | 1,241 | 0,188 | 0,393 | 0,205 | 20,517 |
| 1,241 | 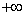 |
0,393 | 0,500 | 0,107 | 10,729 |
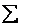 |
1 | 100 |
4. Сравним эмпирические и теоретические частоты, используя критерии Пирсона:
а) вычислим наблюдаемое значение критерия Пирсона. Для этого составим расчетную таблицу .
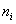 |
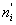 |
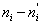 |
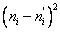 |
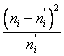 |
| 7,00 | 3,86 | 3,14 | 9,88 | 2,56 |
| 9,00 | 11,64 | -2,64 | 6,96 | 0,60 |
| 18,00 | 24,12 | -6,12 | 37,49 | 1,55 |
| 34,00 | 29,14 | 4,86 | 23,64 | 0,81 |
| 22,00 | 20,52 | 1,48 | 2,20 | 0,11 |
| 10,00 | 10,73 | -0,73 | 0,53 | 0,05 |
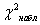 |
5,68 |
б) по таблице критических точек распределения 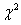 , по уровню значимости α = 0,05 и числу степеней свободы k=s—3 = 6—3 = 3 (s—число интервалов) находим критическую точку правосторонней критической области
, по уровню значимости α = 0,05 и числу степеней свободы k=s—3 = 6—3 = 3 (s—число интервалов) находим критическую точку правосторонней критической области
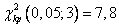 .
.
Так как 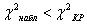 — нет оснований отвергнуть гипотезу о нормальном распределении генеральной совокупности
— нет оснований отвергнуть гипотезу о нормальном распределении генеральной совокупности
Гипотеза согласуется.
18. В процессе исследования среднедушевого дохода (в руб.) обследовано 100 семей. Выявлены оценки: 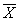 = 1800, s = 230. В предположении о нормальном законе:
= 1800, s = 230. В предположении о нормальном законе:
а) найти долю семей, чей среднедушевой доход находится в пределах от 1200 до 1800;
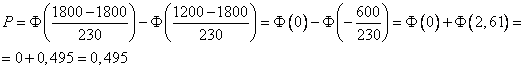
Для того, чтобы найти долю семей, умножим полученную вероятность на 100.
Т.е. 49,5 семей из 100.
Ответ: 49,5 из 100.
б) выяснить при уровне значимости α=0,05 можно ли считать 1900 руб. нормативом среднедушевого дохода (проверить гипотезу H0: а= 1900 против конкурирующей гипотезы Н1: а≠ 1900;
Найдем наблюдаемое значение критерия:
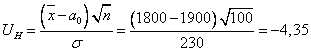
Критическая область двусторонняя, найдем критическую точку из равенства:
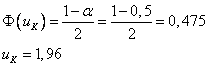
Т.к. 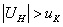 — нулевая гипотеза отвергается, нельзя считать 1900 нормативом.
— нулевая гипотеза отвергается, нельзя считать 1900 нормативом.
в) построить доверительный интервал для оценки неизвестного математического ожидания а и дисперсии σ2 (принять γ = 0,95).
Найдем доверительный интервал для математического ожидания:
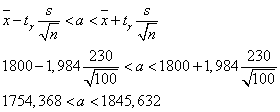
Найдем доверительный интервал для дисперсии:
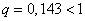 (табличное значение)
(табличное значение)



