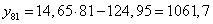19. По данным 16 сотрудников фирмы, где работает 230 человек, среднемесячная заработная плата составила 330 у.е., при s = 100 у.е. Какая минимальная сумма должна быть на счету фирмы, чтобы с вероятностью 0,99 гарантировать выдачу заработной платы всем сотрудникам?
Решение:
Рассчитаем доверительный интервал, в котором будет находиться генеральная средняя величины заработной платы сотрудников.
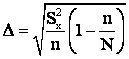
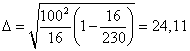
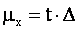
Значение 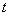 определяем по таблице распределения Лапласа:
определяем по таблице распределения Лапласа:
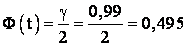 ; t = 2,57
; t = 2,57
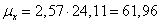
Таким образом, имеем
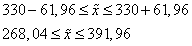
Т.е. среднее значение заработной платы сотрудников генеральной совокупности фирмы с вероятностью 0,95 находится в пределах от 268,04 у.е. до 391,96 у.е.
268,04 ∙ 230 = 61649,2 у.е
Т.е., чтобы с вероятностью γ = 0,95 гарантировать выдачу заработной платы всем сотрудникам, на счету фирмы должно быть минимум 61649,2 у.е.
20. С целью размещения рекламы опрошено 430 телезрителей, из которых данную передачу смотрят 180 человек. С доверительной вероятностью 0,95 найти долю телезрителей, охваченных рекламой в лучшем случае. Случайны ли результаты опроса, если согласно статистике доля телезрителей, охваченных рекламой составляет 0,44 при уровне значимости α=0,05?
Решение:
Доля телезрителей, охваченных рекламой

Средняя ошибка выборки для доли телезрителей рекламы с вероятностью 0,95
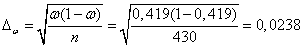
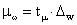
Значение 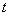 определяем по таблице распределения Лапласа:
определяем по таблице распределения Лапласа:
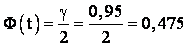 ; t = 1.96
; t = 1.96
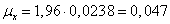
Таким образом, имеем
0,419– 0,047 ≤ ω ≤ 0,419 + 0,047
0,372 ≤ ω ≤ 0,463
Средняя ошибка выборки для доли телезрителей, охваченных рекламой, с вероятностью 0,95 находится в пределах от 0,37 до 0,46.
Результаты опроса не случайны, т.к. 0,44 входит в этот интервал.
21. Распределение пятидесяти предприятий по размерам основных производственных фондов Х (миллионов рублей) и выпуску продукции У (миллионов рублей) дано в таблице:
| 1 | 10 | 19 | 28 | 37 | mxi | |
| 9 | 2 | 3 | – | – | – | 5 |
| 9,3 | 3 | 8 | 2 | – | – | 13 |
| 9,6 | – | 9 | 15 | – | – | 24 |
| 9,9 | – | – | 15 | 11 | ¬– | 26 |
| 10,2 | – | – | 9 | 10 | – | 19 |
| 10,5 | – | – | 3 | 6 | 1 | 10 |
| 10,8 | – | – | – | 1 | 2 | 3 |
| myj | 5 | 20 | 44 | 28 | 3 | n=100 |
Необходимо:
а) вычислить групповые средние 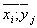 и построить эмпирические линии регрессии;
и построить эмпирические линии регрессии;
Находим групповые средние по формулам:
 , где nij-частоты пар (xi,yj) и ni=
, где nij-частоты пар (xi,yj) и ni=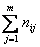 ,m-число интервалов по переменной У.
,m-число интервалов по переменной У.
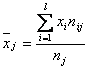 , где nj=
, где nj=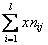 , l-число интервалов по переменной Х.
, l-число интервалов по переменной Х.
Например: 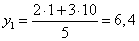 .
.
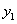 |
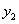 |
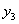 |
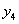 |
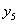 |
||||
| 1 | 10 | 19 | 28 | 37 | ||||
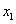 |
9 | 2 | 3 | 5 | 6,40 | |||
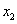 |
9,3 | 3 | 8 | 2 | 13 | 9,31 | ||
 |
9,6 | 9 | 15 | 24 | 15,63 | |||
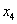 |
9,9 | 15 | 11 | 26 | 22,81 | |||
| x5 | 10,2 | 9 | 10 | 19 | 23,74 | |||
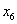 |
10,5 | 3 | 6 | 1 | 10 | 26,20 | ||
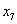 |
10,8 | 1 | 2 | 3 | 34,00 | |||
| 5 | 20 | 44 | 28 | 3 | ||||
| 9,18 | 9,39 | 9,87 | 10,17 | 10,70 |
б) предполагая, что между переменными Х и У существует линейная корреляционная зависимость:
— найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию получившихся уравнений;
— вычислить коэффициент корреляции, на уровне значимости α=0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными Х и У;
— в случае отклонения гипотезы об отсутствии корреляционной зависимости объема выпуска продукции от размера основных производственных фондов оценить меру влияния размера основных производственных фондов на объем выпуска продукции (использовать коэффициент детерминации и корреляционное отношение);
б) По данным таблицы найдем уравнения регрессии У по Х и Х по У:
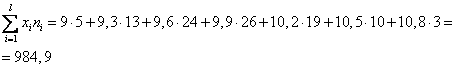
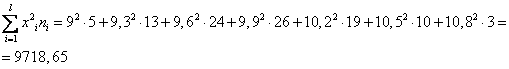

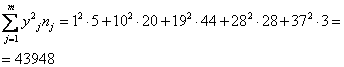
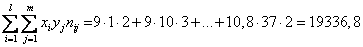
Находим выборочные характеристики и параметры уравнений регрессии:

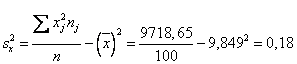

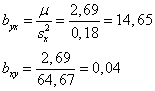
Уравнения регрессии:
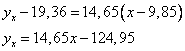
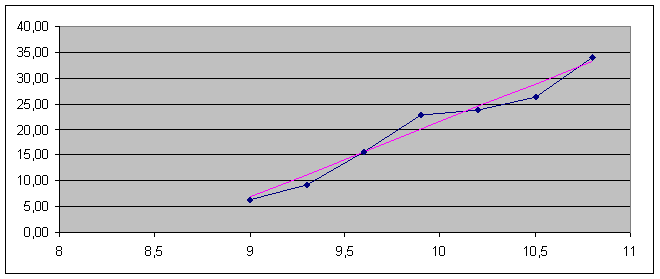
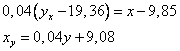
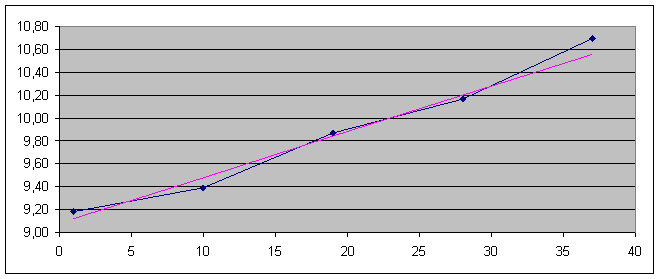
Из первого уравнения регрессии У по Х следует, что при увеличении основных производственных фондов на один млн. руб. выпуск продукции предприятия У увеличивается в среднем на 14,65. Второе уравнение регрессии Х по У показывает, что для увеличения выпуска продукции У на один млн. руб. необходимо в среднем увеличить ОПФ на 0,04.
Находим коэффициент корреляции
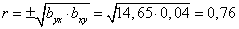 ,
,
Связь между рассматриваемыми переменными прямая и достаточно тесная, r близок к единице.
Оценим значимость коэффициента корреляции:
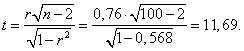
По таблице критерия Стьюдента для уровня значимости 0,05 находим
t (0,95;98)=1,99.
Поскольку t >t(0,95;98), коэффициент корреляции между выпуском продукции У и размерами основных производственных фондов Х значимо отличается от 0.
используя соответствующее уравнение регрессии, оценить средний выпуск продукции предприятий, основные фонды которых составляют 81 млн руб..