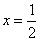Решение уравнений вида: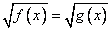 
.
Замечание: практически ничем не отличается от предыдущего типа.
Задача: решить уравнение
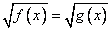
Метод решение:
1) Найдем Область Допустимых Значений переменной, решив систему неравенств
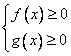
2) Возведем в квадрат обе части уравнения, тем самым избавимся от корня.
3) Решим полученное уравнение
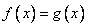
4) Проверим, входят ли полученные корни в Область Допустимых Значений.
5) Сделаем проверку корней, подставив их в исходное уравнение.
Решение уравнений вида: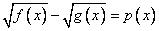 
.
Замечание: Здесь уже интереснее.
Задача: решить уравнение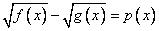
Метод решение:
1) Найдем ограничения на переменную, решив систему неравенств
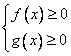
2) Сделаем такие преобразования, чтобы в каждой из частей равенства стояло не более одного корня.
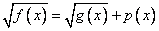
Замечание: Здесь появляются еще ограничения для переменной, правая часть должна быть неотрицательна:
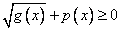
3) Возведем в квадрат обе части уравнения, помним, что
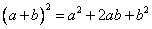и о том, что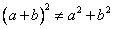 
Получаем уравнение:
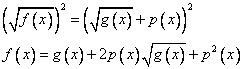
4) Опять преобразуем так, чтобы в одной из частей уравнения осталось только слагаемое, содержащее корень
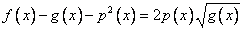
Замечание: Здесь появляются еще ограничения для переменной, обе части равенства должны быть одного знака ( произведение двух сомножителей положительно, если они одно знака, или оба положительны, или оба отрицательны):
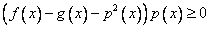
5) Как правило требуется провести какие-то преобразования для понижения степени уравнения, после чего возведем опять обе части в квадрат, корень уйдет, решим полученное уравнение.
6) Проверим, входят ли полученные корни по ограничениям.
Замечание: ограничений тут много, они иногда описываются сложными выражениями, поэтому нужно внимание и проверка (см. п.7)
7) Сделаем проверку корней, подставив их в исходное уравнение.
Пример 3:
Задача: решить уравнение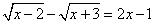 
Решение:
Замечание: Оптимально было бы просто решить это уравнение, возводя его в квадрат и не обращая внимания ни на что, а потом сделать проверку полученных значений переменной.
1) Перенесем второе слагаемое левой части в правую с противоположным знаком.
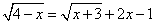
3) Возведем в квадрат обе части уравнения:
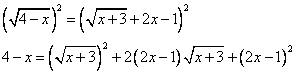
4) Опять преобразуем так, чтобы в одной из частей уравнения осталось только слагаемое, содержащее корень
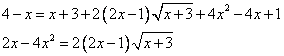
А теперь проведем преобразования этого выражения
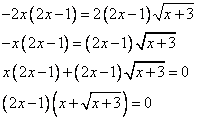
Произведение двух сомножителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
Первый сомножитель:
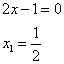
Второй сомножитель
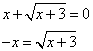
5) Возведем опять обе части в квадрат, корень уйдет, решим полученное уравнение.
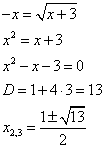
6) Сделаем проверку корней, подставив их в исходное уравнение.
Итак, получили
, 
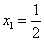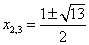
Проверим их.
1)
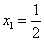
Подставим в исходное уравнение:
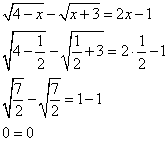
Равенство верное,
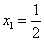является корнем уравнения.2)
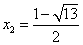
Подставим в исходное уравнение:
Равенство неверное, т.к. корень квадратный не может быть равен отрицательному числу.
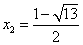не является корнем уравнения.3)
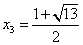
Подставим в исходное уравнение:
Равенство неверное, т.к. корень квадратный не может быть равен отрицательному числу.
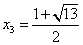не является корнем уравнения.Ответ:
