Оглавление.
1. Метод Крамера.
2. Решение систем уравнений матричным методом (при помощи обратной матрицы).
3. Метод Гаусса решения систем уравнений.
Метод Крамера.
Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ).
Формулы на примере системы из двух уравнений с двумя переменными.
Дано: Решить методом Крамера систему
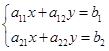
относительно переменных х и у.
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы Вычисление определителей.:
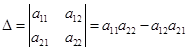
Заменим в этом определителе первый столбец столбцом коэффициентов из правой части системы и найдем его значение:
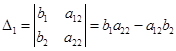
Сделаем аналогичное действие, заменив в первом определителе второй столбец:
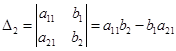
Применим формулы Крамера и найдем значения переменных:
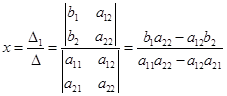и 
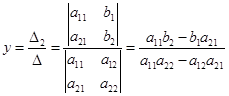.Пример 1:
Решить систему уравнений:
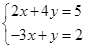
относительно переменных х и у.
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы :
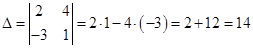
Заменим в этом определителе первый столбец столбцом коэффициентов из правой части системы и найдем его значение:
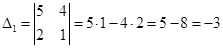
Сделаем аналогичное действие, заменив в первом определителе второй столбец:
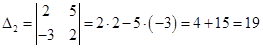
Применим формулы Крамера и найдем значения переменных:
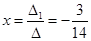и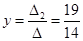 
.Ответ:
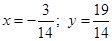
Замечание: Этим методом можно решать системы и большей размерности.
Замечание: Если получается, что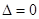 
, а делить на ноль нельзя, то говорят, что система не имеет единственного решения. В этом случае система имеет или бесконечно много решений или не имеет решений вообще.
Пример 2 (бесконечное количество решений):
Решить систему уравнений:
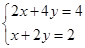
относительно переменных х и у.
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы :
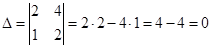
Применять формулы Крамера нельзя. Решим эту систему методом подстановки Решение систем методом подстановки.
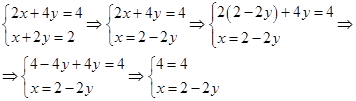
Первое из уравнений системы — равенство, верное при любых значениях переменных (потому что 4 всегда равно 4). Значит, остается только одно уравнение. Это уравнение связи между переменными
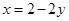.Получили, решением системы являются любые пары значений переменных, связанных между собой равенством
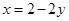.Общее решение запишется так:
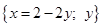
Частные решения можно определять выбирая произвольное значение у и вычисляя х по этому равенству связи.
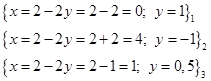
и т.д.
Таких решений бесконечно много.
Ответ: общее решение
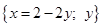
Частные решения:
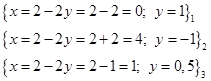
Пример 3 (решений нет, система несовместна):
Решить систему уравнений:
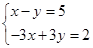
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы :
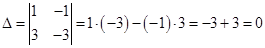
Применять формулы Крамера нельзя. Решим эту систему методом подстановки
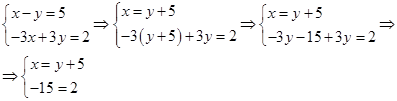
Второе уравнение системы — равенство, неверное ни при каких значениях переменных (конечно же, так как -15 не равно 2). Если одно из уравнений системы не верно ни при каких значениях переменных, то и вся системы не имеет решений.
Ответ: решений нет