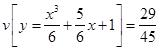Алгоритм нахождения экстремума функционала, как и в ситуации с функциями (ССЫЛКА), состоит из двух шагов:
А) необходимое условие экстремума
Б) достаточное условие экстремума.
Вот что на эту тему говорит Лев Эрнестович Эльсгольц (часть таблицы, условия, применяемые наиболее часто):
Пусть дан функционал вида 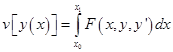 с условиями
с условиями 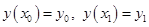 ,
,
| Слабый минимум | Сильный минимум |
| 1. Необходимое условие. Функционал может достигать своего экстремального значения только на функциях, являющихся решением уравнения Эйлера: 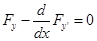 . .Решения этого уравнения называются допустимыми экстремалями. |
1. Необходимое условие. Функционал может достигать своего экстремального значения только на функциях, являющихся решением уравнения Эйлера: 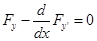 . .
|
| 2. Необходимые условия Если на допустимой экстремали А) выполняется условие Якоби (см. после таблицы), Б) 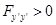 (Условие Лежандра), (Условие Лежандра),то на этой экстремали функционал достигает слабого минимума. |
2. Необходимые условия Если на допустимой экстремали А) выполняется условие Якоби (см. после таблицы), Б) 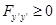 для точек для точек 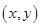 , близких к точкам на исследуемой экстремали и для произвольных значение , близких к точкам на исследуемой экстремали и для произвольных значение 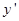 . При этом предполагается, что функция . При этом предполагается, что функция 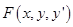 трижды дифференцируема по трижды дифференцируема по 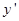 для любых для любых 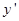 , ,то на этой экстремали функционал достигает сильного минимума. |
Замечание 1: Условия для максимума аналогичны, следует лишь заменить знаки неравенств на противоположные.
Замечание 2:
Уравнение Якоби:
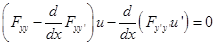 ,
,где
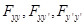 являются известными функциями переменной
являются известными функциями переменной 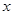 .
.Условие Якоби выполнено, если решение уравнения Якоби
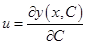 обращаются в ноль при
обращаются в ноль при 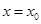 и более не обращаются в ноль ни в одной точке отрезка
и более не обращаются в ноль ни в одной точке отрезка 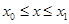 .
.
Все эти замечательные условия лучше всего понимать на примерах.
Задача: Исследовать функционал на экстремум и вычислить экстремальное значение.
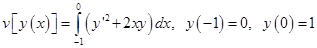
1) Необходимое условие экстремума.
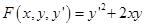
Составим и решим уравнение Эйлера.
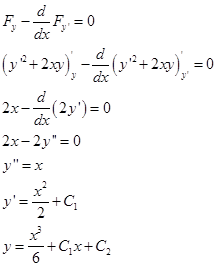
Определим константы из условий
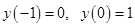
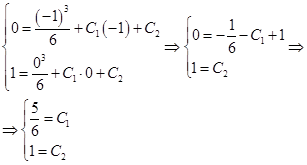
Тогда допустимая экстремаль имеет вид:
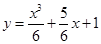
2) Достаточные условия экстремума
А) Условие Якоби.
Запишем и решим уравнение Якоби для
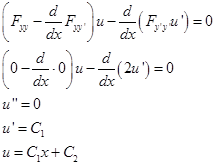
Пусть решение уравнения
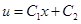 при
при 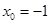 обращается в ноль:
обращается в ноль: 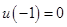 , тогда соотношение констант:
, тогда соотношение констант: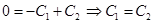
и решение уравнения Якоби можно записать в виде:
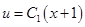 .
.На отрезке
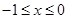 эта функция в ноль более не обращается, т.е. условие Якоби для этой допустимой экстремали (а так получилось, что она тут и не рассматривалась, т.е. оно выполнилось бы для любой экстремали) выполнено.
эта функция в ноль более не обращается, т.е. условие Якоби для этой допустимой экстремали (а так получилось, что она тут и не рассматривалась, т.е. оно выполнилось бы для любой экстремали) выполнено.Замечание: при составлении уравнения Якоби «ушли»
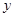 и
и 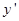 и оно получилось очень простое. Если они не уходят, то следует поставить вместо
и оно получилось очень простое. Если они не уходят, то следует поставить вместо 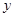 функцию допустимой экстремали, мы ж её исследуем.
функцию допустимой экстремали, мы ж её исследуем.Б) Условие Лежандра.
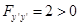 , это неравенство не зависит от
, это неравенство не зависит от 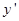 .
.Вывод: на экстремали
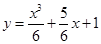 функционал
функционал 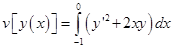 достигает сильного минимума.
достигает сильного минимума.Найдем экстремальное значение функционала:
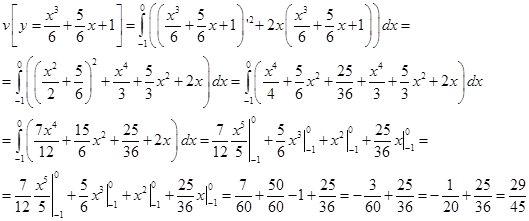
Ответ: Функционал достигает сильного минимума на экстремали
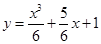 и принимает на ней экстремальное значение
и принимает на ней экстремальное значение