Постановка задачи: Дана поверхность 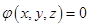 и две точки
и две точки 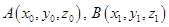 на ней.
на ней.
Требуется определить линию наименьшей длины, соединяющую эти точки и проходящую по этой поверхности.
Общие рассуждения.
1) Линия, т.е. уравнение кривой в пространстве, есть функция трех координат. И ее длину следует минимизировать. Из курса математического анализа помнится, что длина участка кривой вычисляется по формуле:
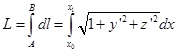 ,
, И требуется минимизировать этот функционал при условии, что
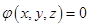 . Получили задачу на условный экстремум функционала:
. Получили задачу на условный экстремум функционала: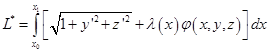 .
.Решая, эту задачу обычным методом, получим в результате функции
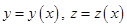 , т.е. искомую кривую.
, т.е. искомую кривую.Это самый общий случай метода решения геодезической задачи и он не очень удобен.
Рассмотрим более простой случай.
Предположим, что уравнение поверхности или задано в параметрической форме, или его можно параметризовать:
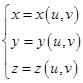
Тогда длину кривой вычислим по формуле:
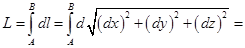
Вспомним формулу для полного дифференциала
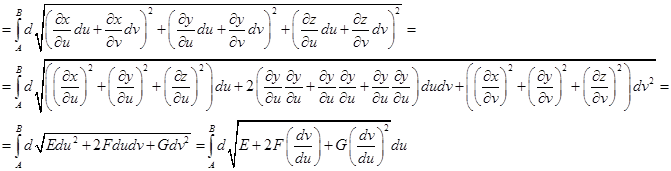
Будем считать, что параметры зависят между собой следующим образом:
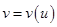 , тогда длина кривой вычисляется по формуле:
, тогда длина кривой вычисляется по формуле: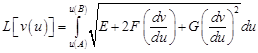 ,
,где
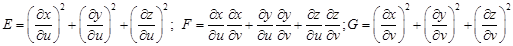
Требуется найти минимум этого функционала при условии, что
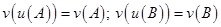 .
.Пример:
Решить задачу о геодезических линиях на примере вычисления расстояния между точками
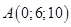 и
и 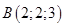 на плоскости
на плоскости 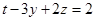
Решение:
Замечание: Если плоскость задана своим общим уравнением
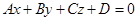 , то неколлинеарные векторы, лежащие в этой плоскости, находятся по формулам:
, то неколлинеарные векторы, лежащие в этой плоскости, находятся по формулам: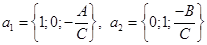 .
.Уравнение плоскости в параметрическом виде :
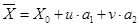
Параметризуем плоскость
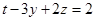 .
.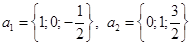
Выберем за точку приложения векторов
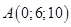
Составим параметрическое уравнение плоскости
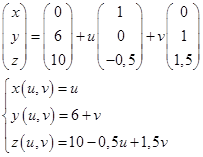
Вычислим составляющие подкоренного выражения:
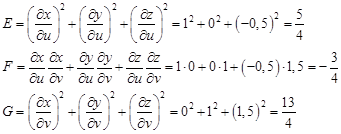
Разберемся с пределами интегрирования и граничными условиями:
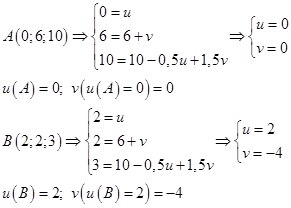
Получили основную задачу вариационного исчисления в виде:
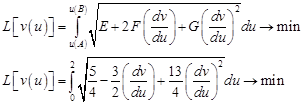
При условиях 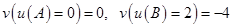
Немного преобразуем функционал перед исследованием на экстремум
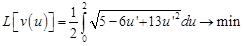
Необходимое условие экстремума.
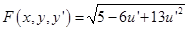
Составим и решим уравнение Эйлера.
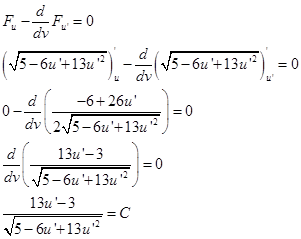
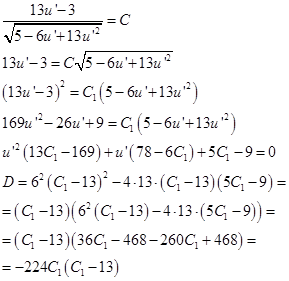
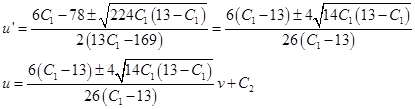
Из области допустимых значений этого уравнения понимаем, что подходит только значение с «+»
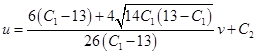
Определим константы из условий 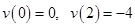
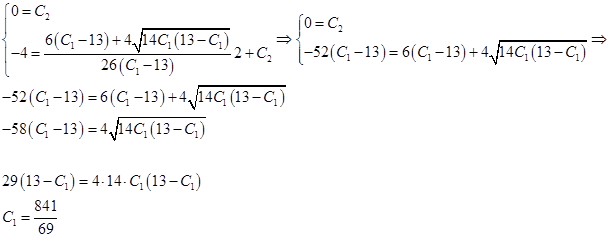
Подставим в выражение для
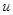 :
: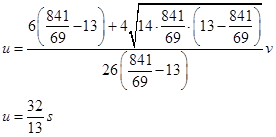
Это допустимая экстремаль, но, по смыслу задачи, других вариантов нет, и будем считать, без проверки достаточных условий экстремума, что функционал достигает на этой экстремали своего минимума (просто составление уравнения Якоби для этого функционала займет много места и времени).
Найдем значение функционала на этой экстремали:
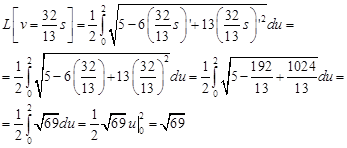
Найдем расстояние между точками
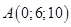 и
и 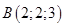 по формуле из геометрии:
по формуле из геометрии: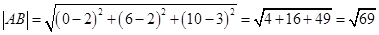
Результаты совпали, значит, вычисления произведены верно.
Ответ:
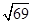



[…] Задача о геодезических линиях. […]