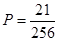16. Монета бросается до тех пор, пока герб не выпадет 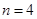раза. Определить вероятность того, что цифра выпадет 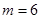раз.
Решение:
По условию задачи герб должен выпасть 4 раза, а решка – 6 раз, значит, всего бросков должно быть 10 штук.
Таким образом, требуется найти вероятность такого события, что из первых девяти бросков выпало 3 герба, и на 10-ый бросок также выпал герб.
Обозначим события:
А – «из 9 бросков выпало 3 герба»
В — «на 10-ый бросок выпал герб».
При этом 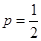— вероятность того, что при одном броске выпадет герб.
Для определения вероятности события А используем формулу Бернулли:

,
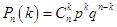где n – количество экспериментов, k – количество благоприятных исходов, p – вероятность благоприятного исхода. Подставим .

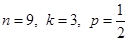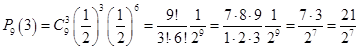
С вероятностью события В немного проще:

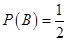
Тогда, по теоремам умножения и сложения вероятностей:

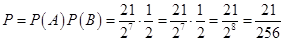
Ответ: