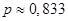13. В первой урне 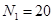белых шаров и 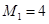черных шара, во второй урне 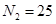белых и 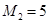черных шара. Из первой урны переложили 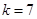шаров. Затем из второй урны извлекли шар. Определить вероятность того, что он белый (событие А).
Решение:
Задача решается по формуле полной вероятности:

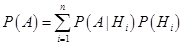
В данном случае в первом ящике 4 черных шара, значит минимальное количество белых из перекладываемых семи шаров может быть только 3 шара.
Обозначим гипотезы:
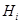— среди переложенных из первой урны во вторую семи шаров 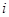шаров белые, .
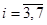Найдем вероятности этих гипотез:

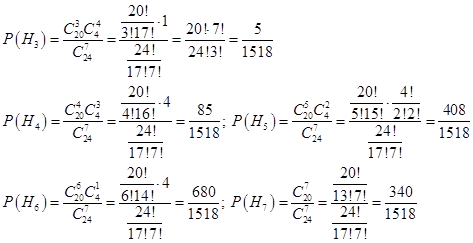
Условные вероятности:
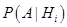— вероятность достать белый шар из второй урны при условии, что среди переложенных в нее было i белых.
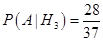— т.к. во втором стало 28 белых и 37 всего.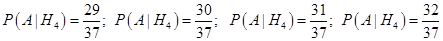

Подставим все в формулу полной вероятности:

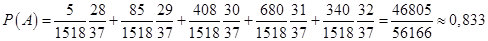
Ответ: