1. Бросаются две игральные кости. Определить вероятность того, что
а) сумма числа очков не превосходит числа 15;
б) произведение числа очков не превосходит числа 15;
в) произведение числа очков делится на 15.
Решение:
Будем решать эту задачу с помощью классического определения вероятности.
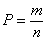, где
n— количество всевозможных исходов.
m— количество благоприятных исходов.
Распишем всевозможные исходы эксперимента. Например (2,4) будет означать, что на первой кости выпала 2, а на второй 4.

(1,1)	(2,1)	(3,1)	(4,1)	(5,1)	(6,1)
(1,2)	(2,2)	(3,2)	(4,2)	(5,2)	(6,2)
(1,3)	(2,3)	(3,3)	(4,3)	(5,3)	(6,3)
(1,4)	(2,4)	(3,4)	(4,4)	(5,4)	(6,4)
(1,5)	(2,5)	(3,5)	(4,5)	(5,5)	(6,5)
(1,6)	(2,6)	(3,6)	(4,5)	(5,6)	(6,6)

Всего – 36 вариантов, т.е. n=36.
А) сумма числа очков не превосходит числа 15. Вообще то сумма на двух костях может быть максимум равна 12, т.е. подходят все пары, т.е. m=36.

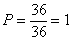
б) произведение числа очков не превосходит числа 15. Подходят пары :

(1,1)*	(2,1)*	(3,1)*	(4,1)*	(5,1)*	(6,1)*
(1,2)*	(2,2)*	(3,2)*	(4,2)*	(5,2)*	(6,2)*
(1,3)*	(2,3)*	(3,3)*	(4,3)*	(5,3)	(6,3)
(1,4)*	(2,4)*	(3,4)*	(4,4)	(5,4)	(6,4)
(1,5)*	(2,5)*	(3,5)	(4,5)	(5,5)	(6,5)
(1,6)*	(2,6)*	(3,6)	(4,5)	(5,6)	(6,6)

Т.е. 23 пары. m = 23.

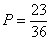
в) произведение числа очков делится на 15. Т.е. это, например, числа 15,30,45, и т.д.
Пары, произведение в которых равно этим цифрам это :

(1,1)	(2,1)	(3,1)	(4,1)	(5,1)	(6,1)
(1,2)	(2,2)	(3,2)	(4,2)	(5,2)	(6,2)
(1,3)	(2,3)	(3,3)	(4,3)	(5,3)*	(6,3)
(1,4)	(2,4)	(3,4)	(4,4)	(5,4)	(6,4)
(1,5)	(2,5)	(3,5)*	(4,5)	(5,5)	(6,5)*
(1,6)	(2,6)	(3,6)	(4,5)	(5,6)*	(6,6)

Т.е., в данном случае m=4

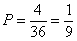
Ответ: а) 1 б) 23/36 в) 1/9