4. В лифт 10-ти этажного дома сели 6 пассажиров. Каждый независимо от других с одинаковой вероятностью может выйти на любом (начиная со второго) этаже. Определить вероятность того, что:
а) все вышли на разных этажах;
б) по крайней мере, двое сошли на одном этаже.
Решение:

.
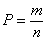n- количество способов, которыми все люди могут выйти на любых этажах.
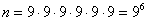, т.к. каждый из 6-ти человек может выйти на любом из 9-ти имеющихся в доме этажей, т.к. на первом они не выходят.
А) все вышли на разных этажах.
m-количество способов выходя людей так, чтобы ни на одном этаже не вышли 2 человека.
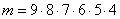, т.к., допустим, первый человек может выйти на любом из девяти этажей, у второго выбор уже на 1 этаж меньше, т.е. 8 вариантов, т.к. на одном этаже первый уже вышел, у третьего пассажира осталось для выхода всего 7 этажей и т.д.
.
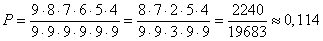Б) по крайней мере, двое сошли на одном этаже.
Событие «по крайней мере, двое сошли на одном этаже» противоположно событию «все сошли на разных этажах». Воспользуемся формулой вероятности противоположного события


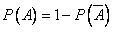
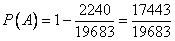
Ответ: , .
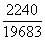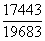