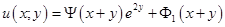2. Найти общее решение уравнения, приведя его к каноническому виду

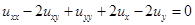
Решение:
Составим характеристическое уравнение и решим его.

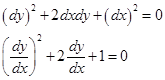
Это квадратное уравнение относительно .
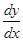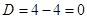— это уравнение параболического типа.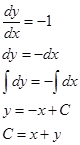

Сделаем замену переменных. Первую возьмем из общего интеграла характеристического уравнения:
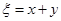, а для замены второй переменной выберем функцию так, чтобы они с 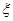были линейно независимы. Например: .
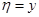Проверим линейную независимость замены:
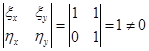— все хорошо.
Итак, замена:
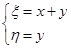
Сделаем замену частных производных.
Подготовительный момент:

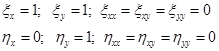
Теперь поставляем в замены:

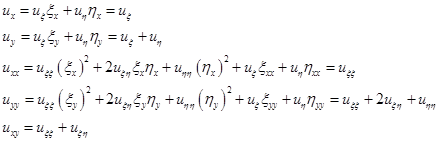
Подставим в исходное уравнение:

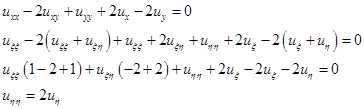
Это каноническое уравнение параболического типа, где .
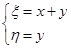Решим его.
Проинтегрируем обе части равенства по :

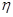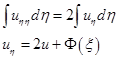
Получили ОДУ, общий вид решения которого (при 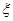считаемой за константу):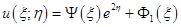

Проверить это можно дифференцированием по 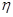и подстановкой в равенство .
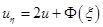Делаем обратную замену и получаем ответ: