Задача: Выполнить три итерации по методу Зейделя для системы уравнений.

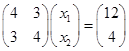
Решение:
Матрица коэффициентов уже готова к применению метода Зейделя, т.к. она диагонально доминирующая, т.к. коэффициенты, стоящие на главной диагонали по модулю максимальные в своей строке, т.е. переставлять строки или делать замену переменной не требуется.
Преобразуем систему линейных уравнений к виду системы для метода Зейделя:


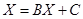
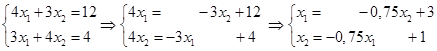
Тогда
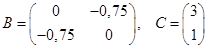
Исследуем на сходимость алгоритма. Для этого найдем норму матрицы В.

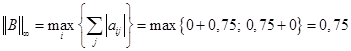
Условие сходимости выполнено, т.к.
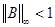
Выберем за начальное приближение нулевой вектор: .
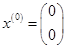Итерационные формулы метода Зейделя:





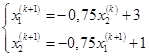
Первая итерация:

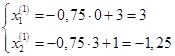
Вторая итерация:

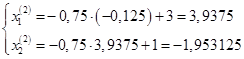
Третья итерация:

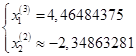
Все, требуемые три итерации провели, на данный момент решение составляет:
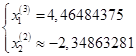
, что кстати не так далеко от истины ( точных значений).
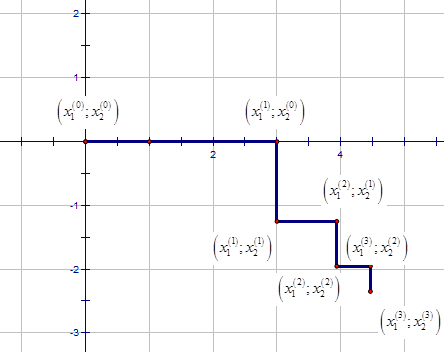
Ну и небольшая картинка на эту тему, то есть изображение итерационного процесса метода Зейделя.