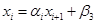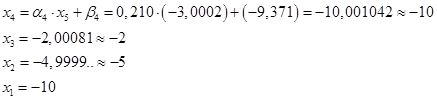Задача: Решить систему линейных алгебраических уравнений методом прогонки.
СЛАУ задана расширенной матрицей коэффициентов:

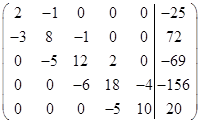
Решение:
Замечание: при записи результатов отображать будем только 3 цифры после запятой
Метод прогонки является упрощенным методом Гаусса и применяется к трехдиагональным матрицам. В условии этой задачи система задана именно такой матрицей, т.е. ненулевые элементы стоят на главной диагонали и на двух её окружающих.
Общий вид уравнение в системе:
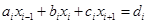
Прямой ход:
1)

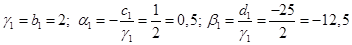
2)

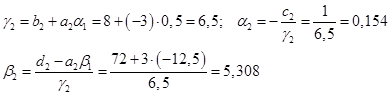
3)

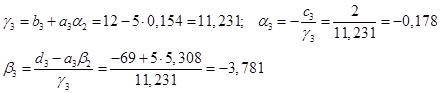
4)

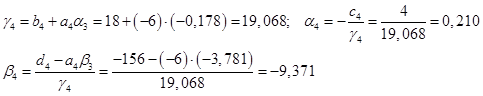
5)





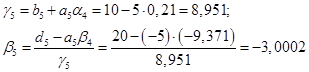
После прямого хода расширенная матрица коэффициентов принимает вид:

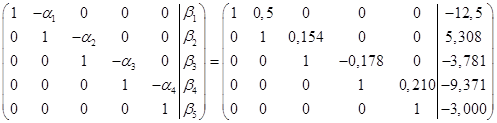
Получили, что 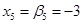, формула для обратного хода: