Задача: Доказать тождество .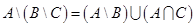
Решение:

Обычно задачи такого плана задаются при изучении науки «Теория вероятностей» в ее первых главах, на тему «Операции над множествами». Решать эту задачу можно несколькими способами:
1) Исходя из непосредственного определения операций, т.е. логически определять при каких условиях элемент будет принадлежать множеству, определяемому правой частью и левой частью, и, если эти условия совпадают, то тождество признается верным. Но это сложно и муторно, не будем рассматривать этот метод.
2) С помощью диаграмм Эйлера-Венна, графически определяя множества-результаты. Если итоговые картинки совпадают, то тождество верно.
3) при помощи характеристической функции.

Итак:
2) Доказать тождество 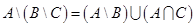с помощью диаграмм Эйлера-Венна, т.е. обозначим графически множества вот так

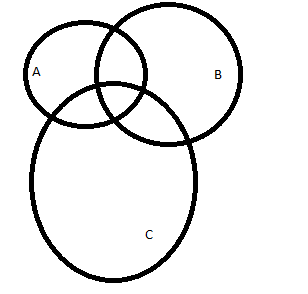
и будем заштриховывать результаты соответствующих операций.

Левая часть:

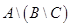
По порядку:
А) 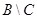(красный цвет):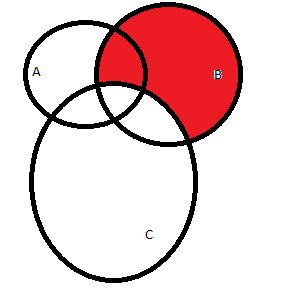

Б) 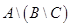(синий цвет):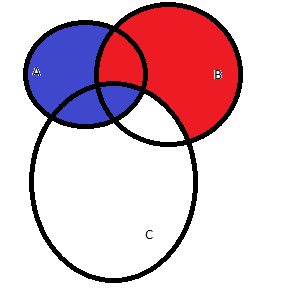

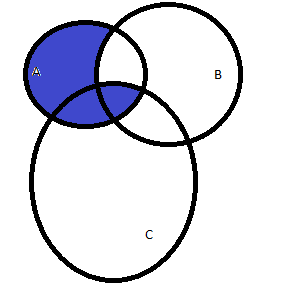
Результат:
:

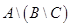Правая часть имеет вид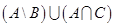
Поехали:
А) 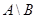(красный):

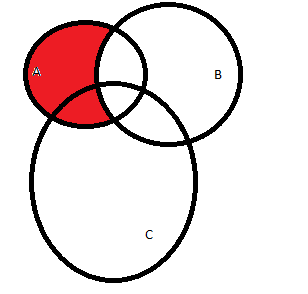
Б) 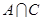(синий):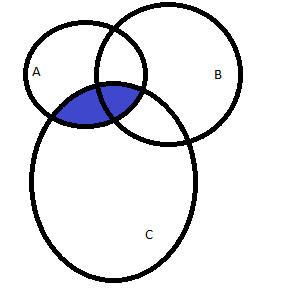

В) Итог 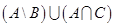(объединение двух последних множеств, обозначим зеленым цветом, хотя, конечно, красный+синий дают фиолетовый.):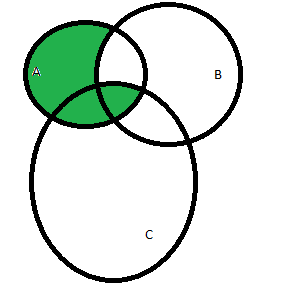

Как легко заметить, закрашенные области для левой и правой частей тождества совпадают, т.е. тождество верно.

3) Доказать тождество с помощью характеристических функций.

Введем понятие характеристической функции.

Определение: Характеристической функцией 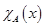множества 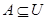называется функция, отображающая множество 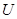на множество :

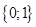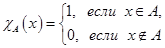
Из определения можно получить следующие равенства:
1) ,
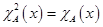2) ,
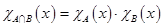3) ,
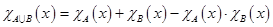4) ,
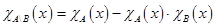5) .

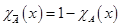Решение методом характеристических функций.

Тождество: .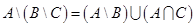

Составим характеристическую функцию левой части тождества:

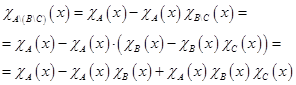
Составим характеристическую функцию левой части тождества:

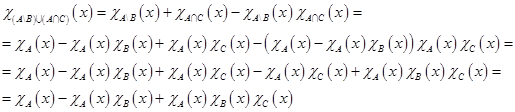
Характеристические функции правой и левой частей тождества совпадают. Следовательно, тождество верно.