Задача: Провести аппроксимацию функции 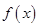, заданной своими значениями, по методу наименьших квадратов с помощью параболы.

x	0	1	2	3	4	5
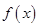	-100	-90	-76	-52	-12	50

Решение: Т.к. в условии требуется аппроксимировать при помощи параболы, то аппроксимирующий многочлен будем искать в виде:
,
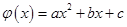а, т.к. требуется его строить по методу наименьших квадратов, то его коэффициенты вычисляются из системы:

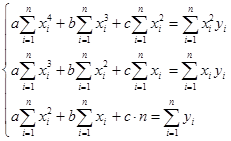
Составим расчётную таблицу:

i	x	y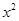
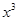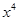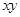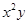1	0	-100	0	0	0	0	0
2	1	-90	1	1	1	-90	-90
3	2	-76	4	8	16	-152	-304
4	3	-52	9	27	81	-156	-468
5	4	-12	16	64	256	-48	-192
6	5	50	25	125	625	250	1250
Сумма:	15	-280	55	225	979	-196	196

Подставим полученные значения в систему:

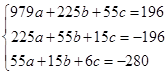
Решать ее можно любым методом, например методом Крамера, тогда:

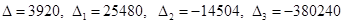
И

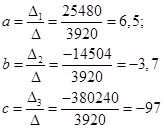
Аппроксимирующая функция примет вид:
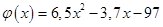
Аналитика: Известно, что исходная функция имеет вид 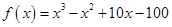. Построим график этой функции и аппроксимирующей в одной системе координат для того, чтобы визуально оценить степень приближенности.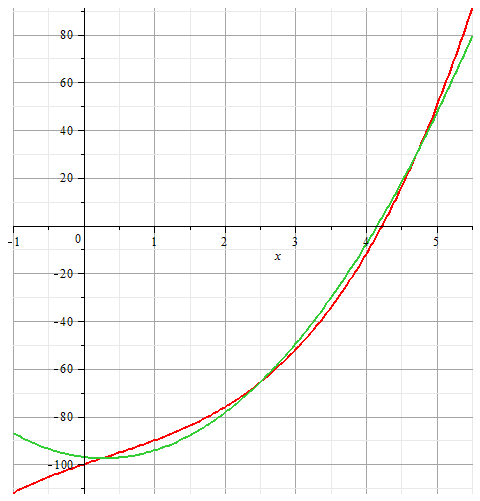

Замечание: как вы понимаете, парабола – зеленая.