Пусть некоторое количество продукции хранится на 3-х складах и у 5-ти магазинов есть потребность в этой продукции. Дана матрица стоимостей перевозок с указанием запасов складов и потребностей магазинов. Требуется венгерским методом решить транспортную задачу и найти оптимальный план перевозок.

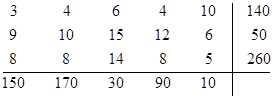
Решение:

Проверим задачу для начала на невырожденность, то есть что предложение складов равно потребностям магазинов:

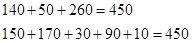
В этой задаче все хорошо.

Приступим непосредственно к венгерскому методу.

Шаг 1. Преобразуем матрицу стоимостей, вычитая из элементов каждой строки минимальный элемент этой строки:

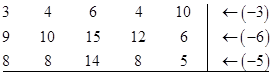
Получим матрицу стоимостей, в которой в каждой строке есть хотя бы один ноль.

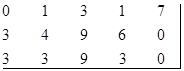
Шаг 2. Вычтем из всех элементов каждого столбца, не содержащего ноль, его минимальный элемент:

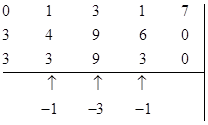
Получили матрицу, где в каждой сроке и в каждом столбце есть по нулю:

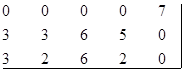
Попробуем распределить перевозки по нулевым клеткам.

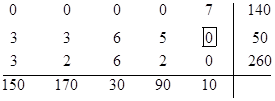
Перевозки по нулевым клеткам распределить невозможно. Обратим внимание на вторую строку, которая содержит ноль только в пятом столбце. Предложение второй строки составляет 50 единиц, а потребность пятого магазина, в который мы можем их направить лишь 10 единиц. Преобразуем матрицу перевозок так, чтобы во второй строке появились еще нули.

Шаг 3. Вычтем из элементов второй строки её минимальный элемент, не принимая в расчет нули. Это элемент 3. Для того, чтобы не появилось отрицательных элементов, прибавим к столбцам, содержащим нули во второй строке этот элемент, т.е. 3.

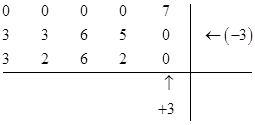
Получим:

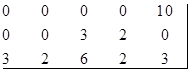
В результате этих операций третья строка стала безнулевой, вычтем из ее элементов минимальный элемент строки, т.е. 2:

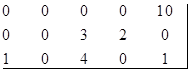
Попробуем опять осуществить перевозки по клеткам, в которых стоят нули.

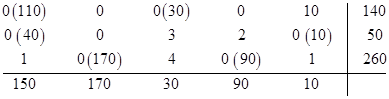
Направим в клетку (2;5) максимальное возможное количество, т.е. min(10;50)=10, получается, что потребности последнего магазина удовлетворены, а на втором складе осталось еще 40 единиц.

Направим в клетку (1;3) максимальное возможное количество, т.е. min(30;140)=30, получается, что потребности третьего магазина удовлетворены, а на первом складе осталось еще 110 единиц.

Обратим внимание, что третий склад предлагает 260 единиц, а в третьей строке нули стоят во втором и четвертом столбцах, потребности которых в сумме составляют как раз 170+90=260. Отправим в ячейку (3;2) 170 единиц и в ячейку (3;4) 90 единиц. Потребности второго и четвертого магазина удовлетворены, с третьего склада все вывезено.

Во второй строке еще осталось 40 единиц, а ноль, допускающий перевозку остался только в первом столбце. Отправим их туда.

Осталось перевезти 110 единиц в клетку (1;1) и план перевозок составлен.

Сопоставим исходную матрицу стоимостей с объемом перевозок и найдем их общую стоимость:

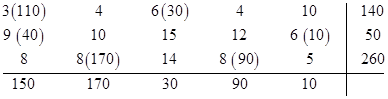
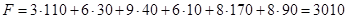
Ответ задачи: план перевозок: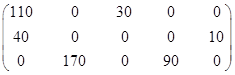
и стоимость 3010 денежных единиц.