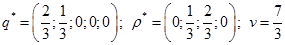Игра задана платежной матрицей. Определить оптимальные стратегии игроков, стратегию первого определить геометрически, а стратегию второго – при помощи симплекс-метода.
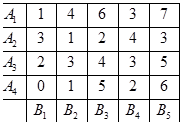
Решение:
Выясним, есть ли тут седловая точка.
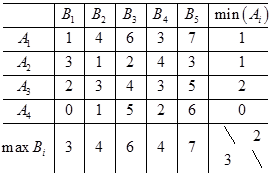
Нижняя цена игры
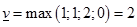
Верхняя цена игры
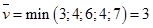
Т.к. нижняя цена не равна верхней цене, то седловой точки нет, т.е. решение матричной игры нужно искать в смешанных стратегиях.
Исследуем матрицу с точки зрения доминирования.
Стратегия
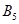 доминирует над стратегией
доминирует над стратегией 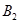 , т.к. все элементы пятого столбца больше соответствующих элементов второго столбца. Уберем пятый столбец.
, т.к. все элементы пятого столбца больше соответствующих элементов второго столбца. Уберем пятый столбец.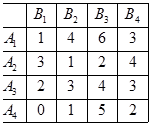
Стратегия
 доминирует над стратегией
доминирует над стратегией  .
.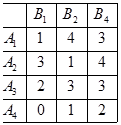
Стратегия  доминирует над стратегией
доминирует над стратегией 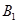 .
.
Стратегия 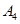 строго доминируется стратегией
строго доминируется стратегией 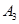 .
.
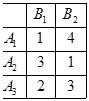
Получили матрицу выигрышей, где у игроков А и В нет доминирующих стратегий.
Сначала найдем оптимальную стратегию игрока В. Заметим, что
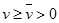 и решим следующую задачу линейного программирования:
и решим следующую задачу линейного программирования:Минимизировать функцию
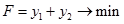 при ограничениях:
при ограничениях: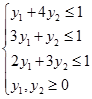
Т.к. переменных всего две, то эту задачу линейного программирования проще всего решить графическим способом. Построим множество допустимых решений, т.е. область, описываемую этими неравенствами и ограниченную прямыми :
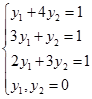
По оси абсцисс будем откладывать
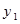 , а по оси ординат
, а по оси ординат 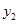 . Область допустимых значений закрашена желтым цветом.
. Область допустимых значений закрашена желтым цветом.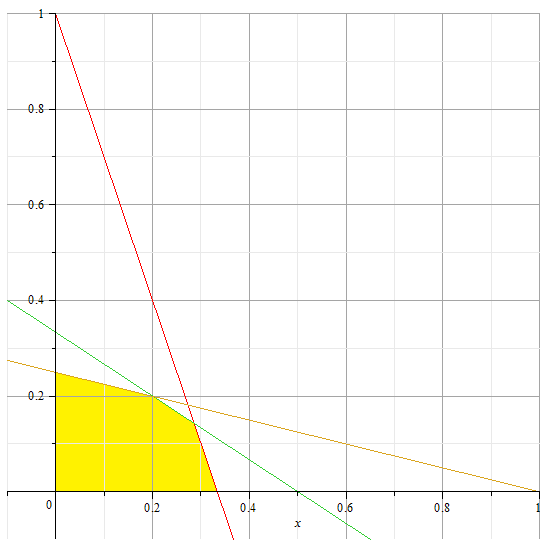
Строим линии уровня
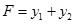 , которые имеют вид
, которые имеют вид 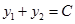 , где С – произвольная постоянная. Понимаем, что для увеличения С прямая должна занимать максимально «высокое» положение, но имея с областью допустимых решений хотя бы одну точку.
, где С – произвольная постоянная. Понимаем, что для увеличения С прямая должна занимать максимально «высокое» положение, но имея с областью допустимых решений хотя бы одну точку.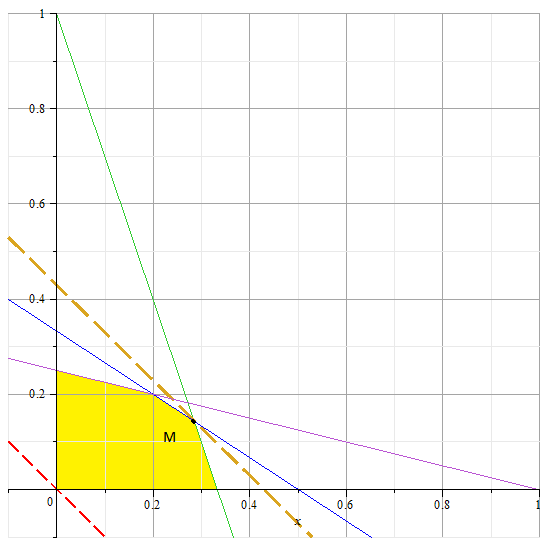
Такое положение прямой – проходящее через точку М. Найдем её координаты как пересечение двух прямых.
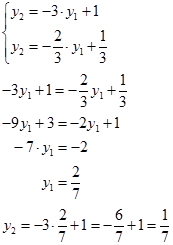
Получили
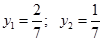 , тогда
, тогда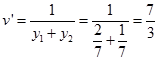 и
и 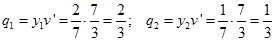
Таким образом оптимальная смешанная стратегия игрока В имеет вид
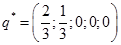 .
.Для нахождения оптимальной стратегии игрока А решаем следующую задачу линейного программирования:
Минимизировать функцию
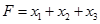 при ограничениях
при ограничениях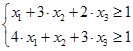
Для решения этой задачи применим симплекс-метод.
Запишем систему ограничений в каноническом для симплекс-метода виде:
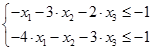
Введем дополнительные переменные
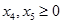 такие, что неравенства преобразуются в равенства
такие, что неравенства преобразуются в равенства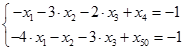
Первый опорный план:
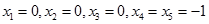
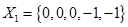 и целевая функция
и целевая функция 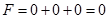 .
.Занесем данные в симплекс –таблицу:
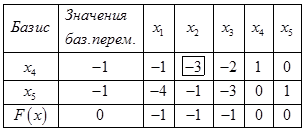
Значение базисных переменных отрицательны, нас такая ситуация не устраивает. Выберем среди значений базисного столбца наибольший по модулю. Оба таких значения равны 1, выберем первую строку (делим элементы целевой строки на элементы выбранной)
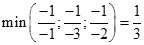
Это значение соответствует второму столбцу, т.е. в базисе
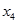 следует вывести, а
следует вывести, а 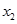 — ввести. Разрешающий элемент (-3), стоящий на пересечении первой строки и второго столбца. Пересчитаем элементы таблицы по методу Жордана-Гаусса. Подробнее об этом можно прочитать тут: Решение производственной задачи симплекс-методом.
— ввести. Разрешающий элемент (-3), стоящий на пересечении первой строки и второго столбца. Пересчитаем элементы таблицы по методу Жордана-Гаусса. Подробнее об этом можно прочитать тут: Решение производственной задачи симплекс-методом.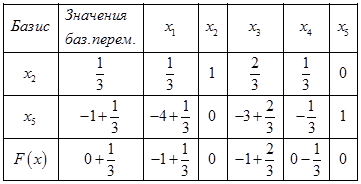
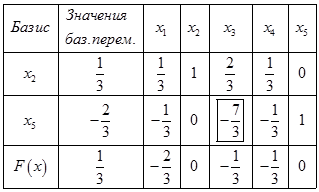
Среди значений базисных переменных присутствуют отрицательные значения, план не является оптимальным. Максимальное значение столбца базисным переменных ( по модулю)
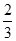 , это соответствует второй строке,
, это соответствует второй строке, 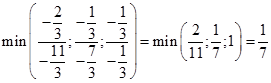 , что соответствует третьему столбцу, т.е. выводим из базиса
, что соответствует третьему столбцу, т.е. выводим из базиса 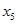 и вводим туда
и вводим туда 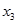 . Пересчитываем.
. Пересчитываем.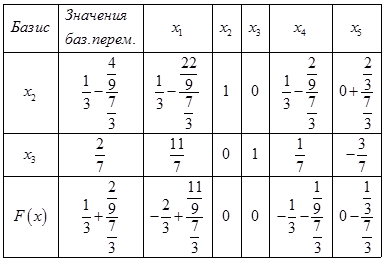
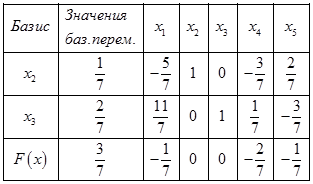
Среди значений базисного столбца нет отрицательных переменных, т.е. получен оптимальный план:
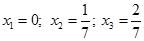 и
и 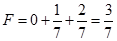 .
.Тогда:
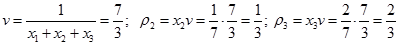
Следовательно, оптимальная смешанная стратегия игрока А имеет вид:
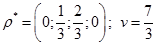 .
.Ответ: Цена игры и стратегии: