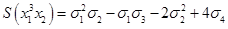Определение: многочлен от нескольких переменных называется симметрическим, если он не изменяется ни при какой перестановке неизвестных.
Пример: 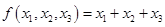, т.к. 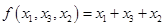— не изменился при перестановке переменных.
Следующие n многочленов от n неизвестных называются элементарными симметрическими:

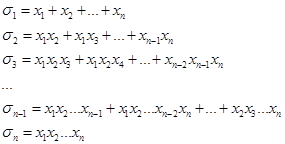
Решим несколько задач на тему симметрических многочленов.
1. Выразить через основные (элементарные) симметрические многочлены выражение:

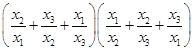
Решение:
Приведем к общему знаменателю, раскроем скобки и приведем подобные слагаемые:

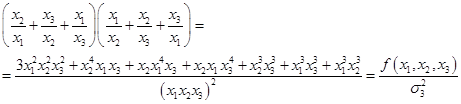
В знаменателе проблем нет, сразу видно, что это 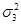, а вот с числителем придется повозиться.

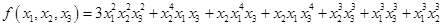
Слагаемое с наибольшим порядком степени здесь вида: 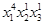, старшая степень 4, сумма степеней 6, будем перебирать наборы из трех степеней, убывающие, первая не больше 4, в сумме дающие 6:

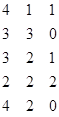
Тогда, каждому набору 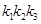, где 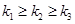будет соответствовать многочлен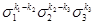
Получим

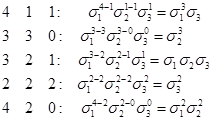
Т.к. Коэффициент при выбранном старшем слагаемом равен 1, то будем искать функцию в виде:

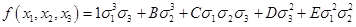
Определим 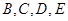методом неопределенных коэффициентов:
1) Пусть ,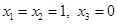
Тогда

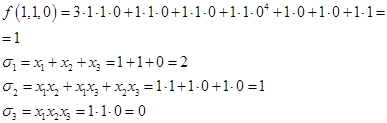
Подставим:

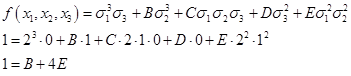
2) Пусть ,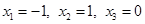
Тогда

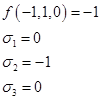
Подставим:

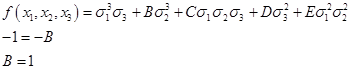
Сразу можно сделать вывод :

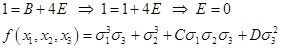
3) Пусть ,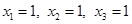
Тогда

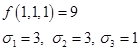
Подставим:

4) Пусть ,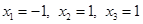
Тогда

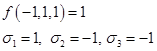
Подставим:

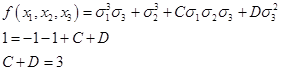
Определим С и D:

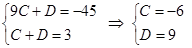
Получили, что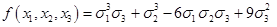
Ответ: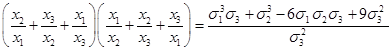

Пример 2.
Выразить через элементарные симметрические многочлены моногенный многочлен
.
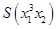Замечание: моногенный многочлен такого вида есть аналогия обозначения основных симметрических многочленов, т.е. в этом случае: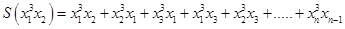

Алгоритм аналогичен приведенному в предыдущей задаче, только без ограничения количества переменных. В многочлене слагаемые имеют вид: 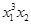, значит старшая степень 3, а сумма степеней 4:

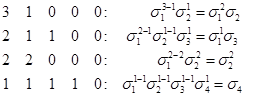
Тогда наш моногенный многочлен можно записать в виде с неопределенными коэффициентами, при этом коэффициент при старшем слагаемом равен 1:

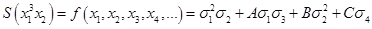
Вычислим коэффициенты:
1) Пусть

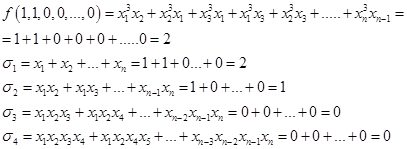
Подставим:

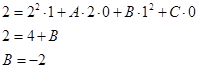
И получим: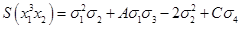
2)

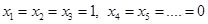
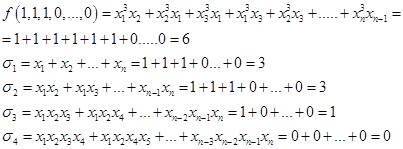
Подставим:

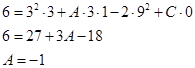
И получим: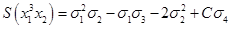
3)

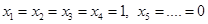
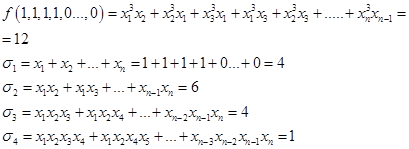
Подставим:

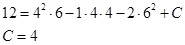
И получим ответ: