Пример 1:
Найти приближённое решение задачи Коши 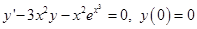методом Эйлера на заданном отрезке 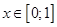с шагом h = 0,1 .
Решение:
Для начала, найдем точное решение этого линейного уравнения первого порядка

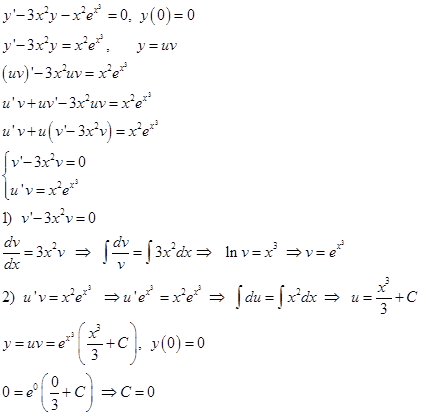
Тогда точное решение имеет вид :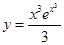
Теперь найдем численное приближенное решение методом Эйлера, с шагом .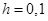

Общий вид: Уравнение 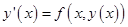, формула: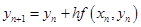
В этом случае :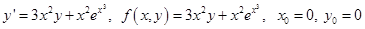
Тогда формулы имеет вид: 6

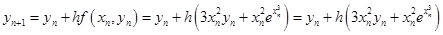
Распишем первые два шага:

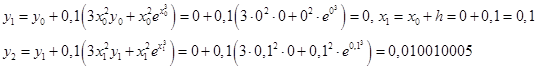
n		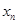	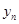Точное значение
0	0	0	0
1	0,1	0	0,000334
2	0,2	0,001001	0,002688
3	0,3	0,005045	0,009246
4	0,4	0,014428	0,022743
5	0,5	0,032178	0,047215
6	0,6	0,062920	0,089359
7	0,7	0,114395	0,161115
8	0,8	0,200260	0,284779
9	0,9	0,345502	0,503741
10	1	0,597372	0,906094

Пример 2:
Найти приближённое решение задачи Коши 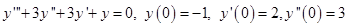методам Эйлера на заданном отрезке 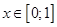с шагом h= 0,01.
Найдем точное решение этого уравнения:

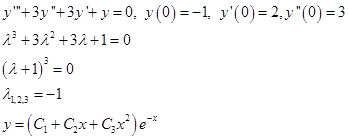
Подстановка начальных условий позволяет определить значение констант и частное решение будет иметь вид:

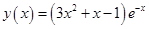
Применим метод Эйлера
Сведем заменой 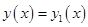переменных это уравнение 3 – го порядка к системе диф. уравнений

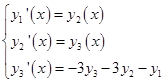
И начальные условия примут вид: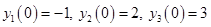
Для системы вида:

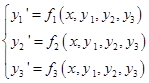
Приближенное решение можно найти по формулам:
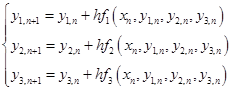, где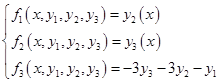
В этом случае:

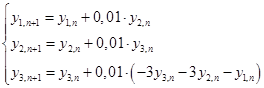
Первая итерация:

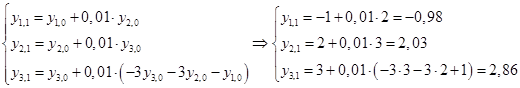
В качестве старта возьмем .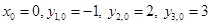
Учитывая замену, следует сравнивать столбцы Точного решения и 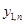. Для краткости приведены не все строки таблицы, обращайте внимание на n.

n		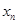		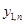	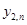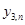Точное значение
0	0	-1	2	3	-1
1	0,01	-0,98	2,03	2,86	-0,97985
2	0,02	-0,9597	2,0586	2,7231	-0,95942
3	0,03	-0,93911	2,085831	2,589246	-0,93871
4	0,04	-0,91826	2,111723	2,458385	-0,91775
5	0,05	-0,89714	2,136307	2,330464	-0,89653
6	0,06	-0,87578	2,159612	2,205432	-0,87509
7	0,07	-0,85418	2,181666	2,083239	-0,85342
8	0,08	-0,83236	2,202499	1,963833	-0,83154
9	0,09	-0,81034	2,222137	1,847167	-0,80947
10	0,1	-0,78812	2,240609	1,733191	-0,78721
20	0,2	-0,55754	2,366848	0,731284	-0,55674
40	0,4	-0,07924	2,369966	-0,64686	-0,08044
50	0,5	0,154261	2,284097	-1,09242	0,151633
60	0,6	0,377332	2,159485	-1,41336	0,373192
70	0,7	0,586627	2,007527	-1,63265	0,581005
80	0,8	0,779844	1,837489	-1,76968	0,772846
90	0,9	0,955524	1,656837	-1,84081	0,947307
100	1	1,112886	1,471524	-1,85974	1,103638

Пример 3.
Решить модифицированным методом Эйлера уравнение: 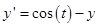на интервале 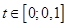и с начальным условием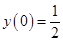
Найдем аналитическое решение уравнения:
Это линейное уравнение первого порядка.

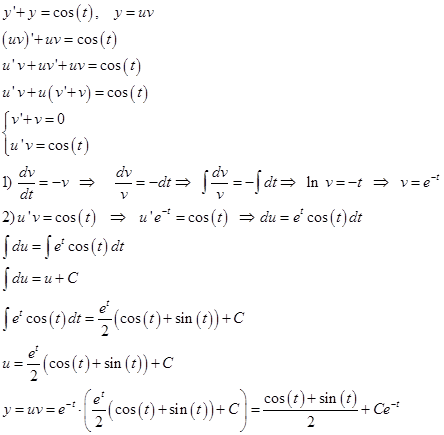
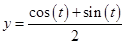
Т.к. 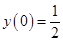, то частным решением этого уравнения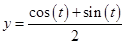
Найдем численное решение уравнения 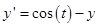, , 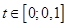модифицированным методом Эйлера с h=0,01;
Формулы:

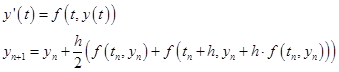
В этом случае:

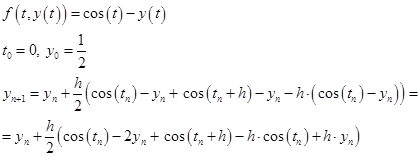
Сделаем «руками» первую итерацию:

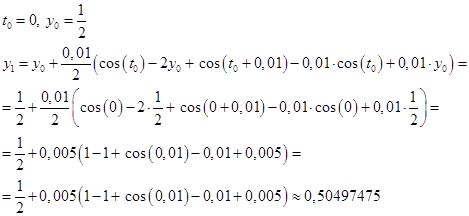
Остальное вычислим компьютерным способом и представим таблицу для

n			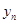Точное решение.
0	0	0,5	0,5
1	0,01	0,50497475	0,504974917
2	0,02	0,509899004	0,509899337
3	0,03	0,514772269	0,514772767
4	0,04	0,519594058	0,51959472
5	0,05	0,524363889	0,524364715
6	0,06	0,529081285	0,529082273
7	0,07	0,533745774	0,533746924
8	0,08	0,538356889	0,5383582
9	0,09	0,54291417	0,542915641
10	0,1	0,547417161	0,547418791