Пример 1. Найти приближённое решение задачи Коши 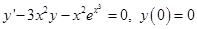 методом Рунге-Кутты 4 порядка на заданном отрезке
методом Рунге-Кутты 4 порядка на заданном отрезке 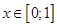 с шагом h = 0,1.
с шагом h = 0,1.
Решение:
Для начала, найдем точное решение этого линейного уравнения первого порядка
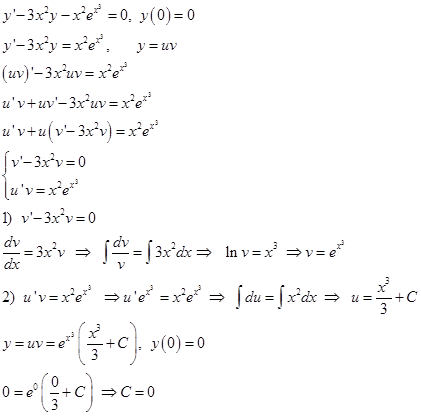
Тогда точное решение имеет вид : 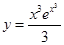
Найдем приблизительное численное решение дифференциального уравнения методом Рунге-Кутты ( Рунге-Кутта ) 4-го порядка.
Формулы для метода Рунге-Кутты:
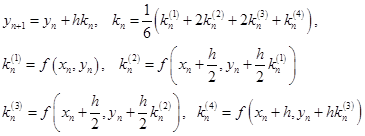
Напомним уравнение:
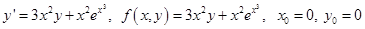
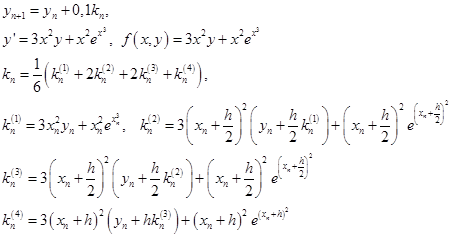
| n | 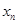 |
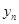 |
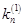 |
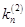 |
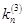 |
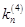 |
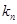 |
Точное значение |
| 0 | 0 | 0 | 0 | 0,0025 | 0,002501 | 0,010018 | 0,003337 | 0 |
| 1 | 0,1 | 0,000334 | 0,01002 | 0,022632 | 0,022675 | 0,040633 | 0,023545 | 0,000334 |
| 2 | 0,2 | 0,002688 | 0,040644 | 0,064369 | 0,064592 | 0,094933 | 0,065583 | 0,002688 |
| 3 | 0,3 | 0,009246 | 0,09496 | 0,133009 | 0,133709 | 0,181431 | 0,134971 | 0,009246 |
| 4 | 0,4 | 0,022744 | 0,181492 | 0,241149 | 0,242961 | 0,318567 | 0,244713 | 0,022743 |
| 5 | 0,5 | 0,047215 | 0,318698 | 0,414566 | 0,418916 | 0,543032 | 0,421449 | 0,047215 |
| 6 | 0,6 | 0,08936 | 0,543305 | 0,703721 | 0,713888 | 0,926793 | 0,717553 | 0,089359 |
| 7 | 0,7 | 0,161115 | 0,927332 | 1,207835 | 1,231503 | 1,61371 | 1,23662 | 0,161115 |
| 8 | 0,8 | 0,284777 | 1,614692 | 2,127454 | 2,183025 | 2,901619 | 2,189545 | 0,284779 |
| 9 | 0,9 | 0,503732 | 2,903203 | 3,884036 | 4,016816 | 5,434521 | 4,023238 | 0,503741 |
| 10 | 1 | 0,906055 | 0,906094 |
Пример 2. Найти приближённое решение задачи Коши 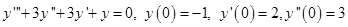 методом Рунге-Кутты 4 порядка на заданном отрезке
методом Рунге-Кутты 4 порядка на заданном отрезке 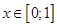 с шагом h = 0,01.
с шагом h = 0,01.
Найдем точное решение этого уравнения:
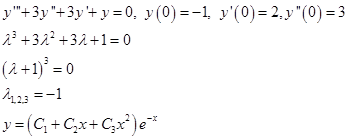
Подстановка начальных условий позволяет определить значение констант и частное решение будет иметь вид:
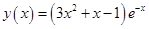
Найдем численное приблизительное решение дифференциального уравнения методом Рунге-Кутты 4-го порядка.
Сведем заменой 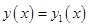 переменных это уравнение 3 – го порядка к системе диф. уравнений
переменных это уравнение 3 – го порядка к системе диф. уравнений
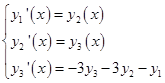
И начальные условия примут вид: 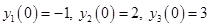
Для системы вида:
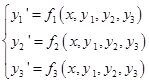
Напомним формулы для этого метода
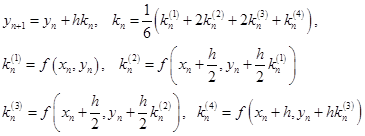
Соответственно, здесь будет:
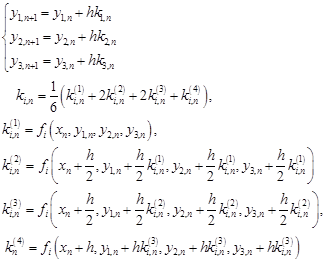
Опять вспомним систему:
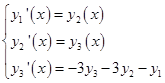 , откуда
, откуда 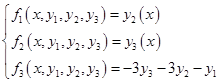
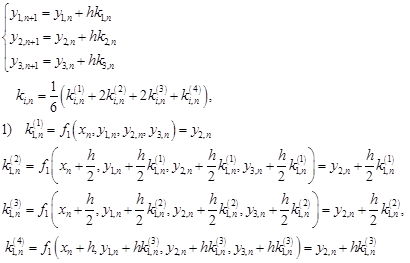
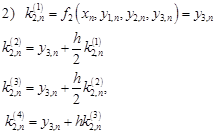
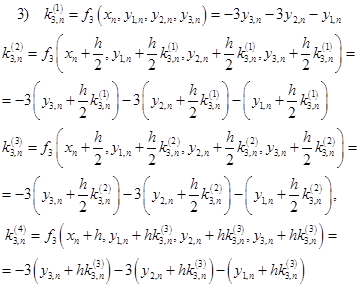
Внимание, в таблице даны не все шаги при h=0,01, обращайте внимание на n.
| n | x | y1 | k1 | y2 | k2 | y3 | k3 | т.З. |
| 0 | 0 | -1,0000 | 2,0100 | 2,0000 | 3,0151 | 3,0000 | -13,5212 | -1,0000 |
| 1 | 0,01 | -0,9799 | 2,0403 | 2,0302 | 2,8792 | 2,8648 | -13,2362 | -0,9799 |
| 2 | 0,02 | -0,9595 | 2,0693 | 2,0589 | 2,7461 | 2,7324 | -12,9559 | -0,9594 |
| 3 | 0,03 | -0,9388 | 2,0969 | 2,0864 | 2,6159 | 2,6029 | -12,6800 | -0,9387 |
| 4 | 0,04 | -0,9178 | 2,1232 | 2,1126 | 2,4885 | 2,4761 | -12,4087 | -0,9177 |
| 5 | 0,05 | -0,8966 | 2,1482 | 2,1374 | 2,3638 | 2,3520 | -12,1418 | -0,8965 |
| 6 | 0,06 | -0,8751 | 2,1719 | 2,1611 | 2,2418 | 2,2306 | -11,8792 | -0,8751 |
| 7 | 0,07 | -0,8534 | 2,1945 | 2,1835 | 2,1224 | 2,1118 | -11,6209 | -0,8534 |
| 8 | 0,08 | -0,8315 | 2,2158 | 2,2047 | 2,0056 | 1,9956 | -11,3669 | -0,8315 |
| 9 | 0,09 | -0,8093 | 2,2359 | 2,2248 | 1,8913 | 1,8819 | -11,1171 | -0,8095 |
| 10 | 0,1 | -0,7869 | 2,2550 | 2,2437 | 1,7796 | 1,7707 | -10,8714 | -0,7872 |
| 20 | 0,2 | -0,5547 | 2,3872 | 2,3753 | 0,7916 | 0,7876 | -8,6287 | -0,5567 |
| 30 | 0,3 | -0,3134 | 2,4300 | 2,4178 | 0,0126 | 0,0125 | -6,7391 | -0,3186 |
| 40 | 0,4 | -0,0711 | 2,4026 | 2,3906 | -0,5907 | -0,5878 | -5,1549 | -0,0804 |
| 50 | 0,5 | 0,1659 | 2,3215 | 2,3099 | -1,0471 | -1,0418 | -3,8344 | 0,1516 |
| 60 | 0,6 | 0,3929 | 2,2002 | 2,1893 | -1,3812 | -1,3743 | -2,7407 | 0,3732 |
| 70 | 0,7 | 0,6063 | 2,0501 | 2,0399 | -1,6145 | -1,6064 | -1,8415 | 0,5810 |
| 80 | 0,8 | 0,8038 | 1,8804 | 1,8710 | -1,7652 | -1,7563 | -1,1087 | 0,7728 |
| 90 | 0,9 | 0,9838 | 1,6987 | 1,6903 | -1,8488 | -1,8395 | -0,5176 | 0,9473 |
| 100 | 1 | 1,1452 | 1,5112 | 1,5037 | -1,8786 | -1,8692 | -0,0469 | 1,1036 |


