Решить задачу о нахождении кратчайшего пути алгоритмом Дейкстры.
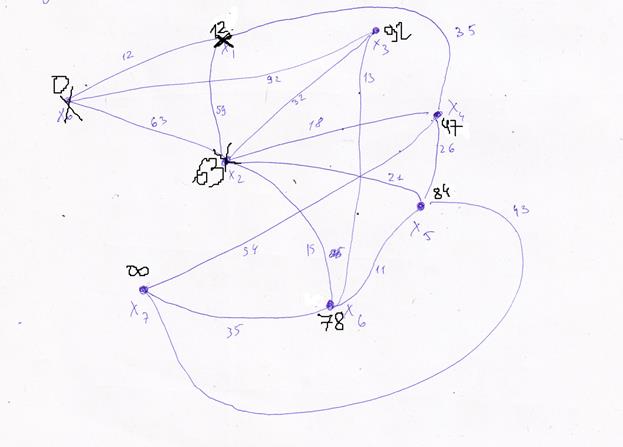
Найти кратчайший путь от Х0 до Х7. Граф задан элементами стоимостной матрицы

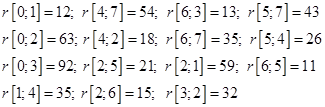
Построим этот граф

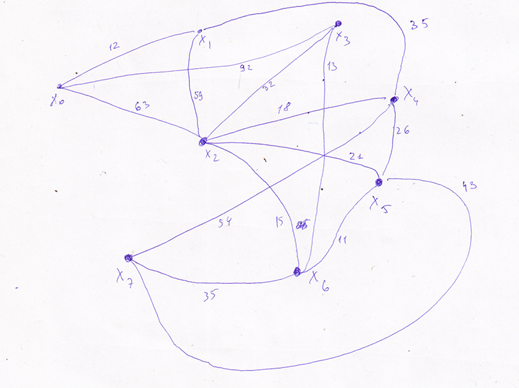
Начнем с элемента Х0 и присвоим ему метку 0, рассмотрим всех его соседей, т.к. там еще нет пометок, то присвоим им соответствующие длины:

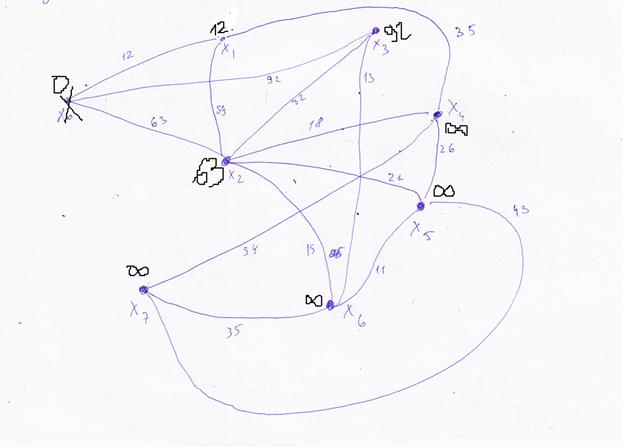
Все соседи Х0 рассмотрены, помечаем ее и переходим к вершине Х1. ЕЕ соседи Х0, Х2,Х4, но Х0 помечена, не рассматриваем ее. Для Х2: 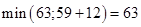, оставляем метку.

Для Х4: 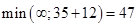, заменяем метку. Все соседи вершины Х1 рассмотрены, помечаем ее

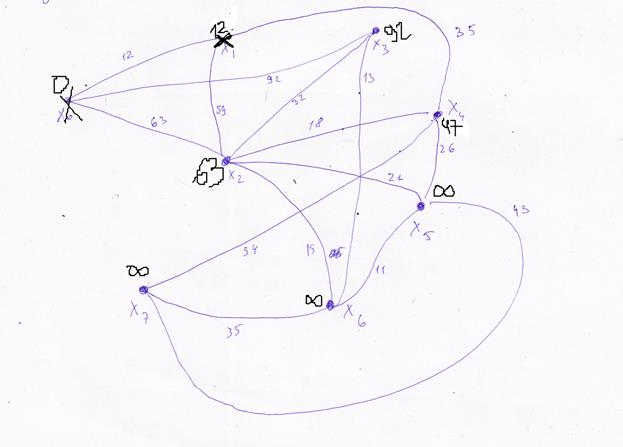
переходим к вершине Х2. ЕЕ соседи Х0, Х1,Х3, Х4, Х5, Х6, но Х0, Х1 помечены, не рассматриваем их.
Для Х3: 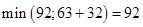, оставляем метку.
Для Х5: 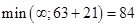, заменяем метку .
Для Х4: 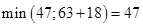, оставляем метку .
Для Х6: 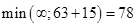, заменяем метку .
Все соседи вершины Х2 рассмотрены, помечаем ее.

переходим к вершине Х3. ЕЕ соседи Х0, Х2, Х6, но Х0, Х2 помечены, не рассматриваем их.
Для Х6: 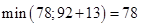, оставляем метку.
Все соседи вершины Х3 рассмотрены, помечаем ее.

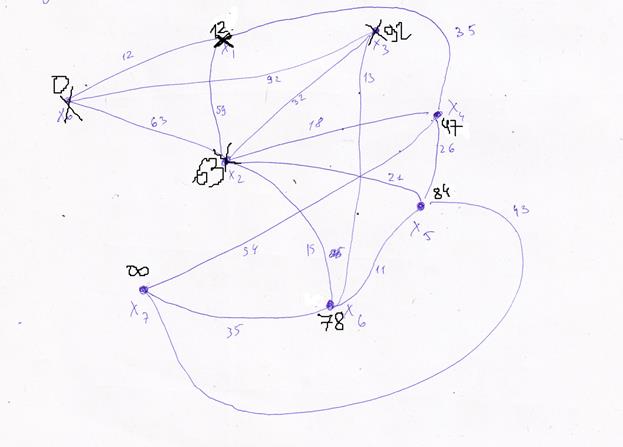
переходим к вершине Х4. ЕЕ соседи Х1,Х2, Х5, Х7, но Х1, Х2 помечены, не рассматриваем их.
Для Х5: 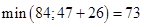, заменяем метку.
Для Х7: 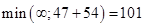, заменяем метку .
Все соседи вершины Х4 рассмотрены, помечаем ее.

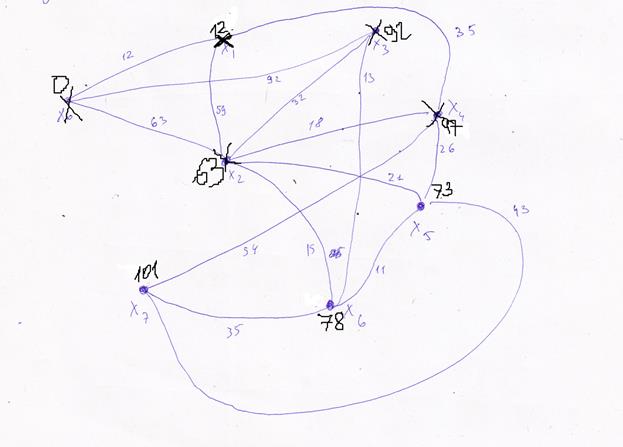
переходим к вершине Х5. ЕЕ соседи Х2,Х4, Х6, Х7, но Х2, Х4 помечены, не рассматриваем их.
Для Х6: 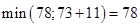, оставляем метку.
Для Х7: 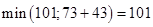, оставляем метку .
Все соседи вершины Х5 рассмотрены, помечаем ее.

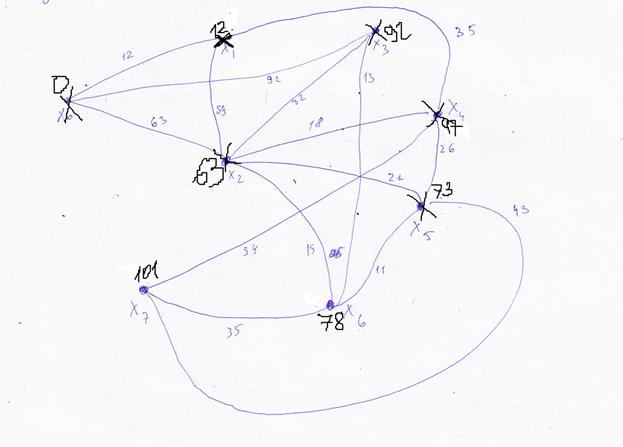
переходим к вершине Х6. ЕЕ соседи Х2,Х3, Х5, Х7, но Х2, Х3, Х5 помечены, не рассматриваем их.
Для Х7: 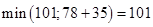, оставляем метку .
Все соседи вершины Х6 рассмотрены, помечаем ее. И помечаем оставшуюся Х7, все вершины рассмотрены.

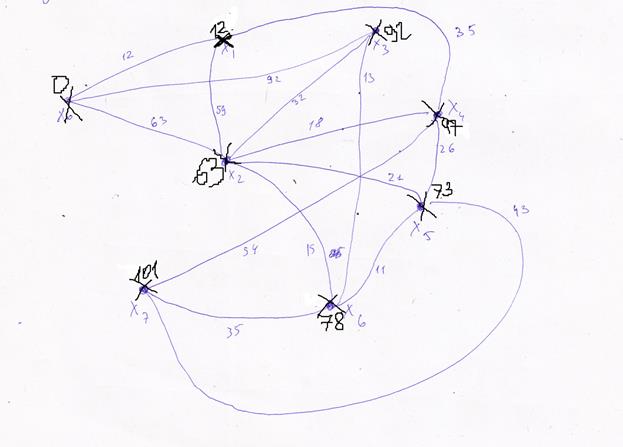
Вывод: Кратчайший путь их Х0 в Х7 имеет длину 101, этот путь: Х7-Х4-Х1-Х0.