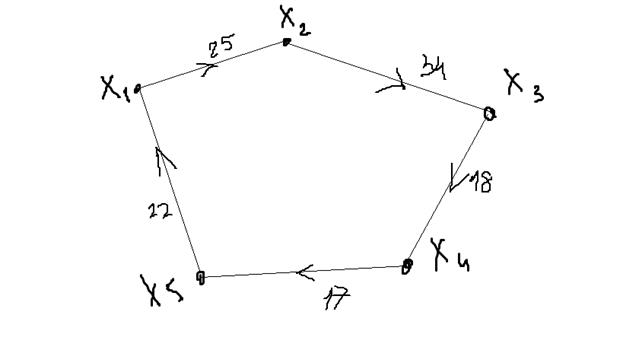
Решить задачу о коммивояжёре, т.е. найти гамильтонов цикл минимальной стоимости.
Выберем один из точных алгоритмов, а именно, венгерский алгоритм.
Условие:

Значения элементов матрицы расстояний:
a(1.1)= ∞ ; a(2.1)=53; a(3.1)=32; a(4.1)=21; a(5.1)=22
a(1.2)=25; a(2.2)= ∞; a(3.2)=72; a(4.2)=45; a(5.2)=43
a(1.3)=15; a(2.3)=34; a(3.3)= ∞; a(4.3)=29; a(5.3)=34
a(1.4)=18; a(2.4)=36; a(3.4)=18; a(4.4)= ∞; a(5.4)=46
a(1.5)=46; a(2.5)=75; a(3.5)=24; a(4.5)= 17; a(5.5)= ∞
Решение:

Составим таблицу длин ребер

Выберем минимальный элемент в каждой строке и вычтем его из каждого элемента соответствующей строке.

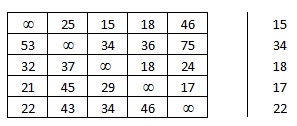
Вычтем.

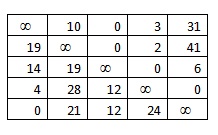
Во втором столбце нет нуля, минимальный элемент этого столбца равен 10, вычтем его из всего столбца.

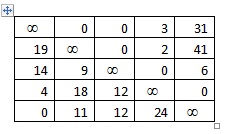
Полученная матрица содержит нули в каждом столбце и каждой строке. Попробуем по ним составить путь коммивояжера ( гамильтонов цикл)
1) Элемент (5;1)=0, убираем пятую строку и первый столбец.

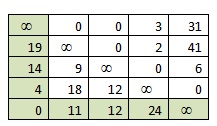
2) Элемент (4;5)=0, убираем четвертую строку и пятый столбец.

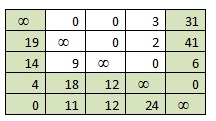
3) Элемент (3;4)=0, убираем третью строку и четвертый столбец.

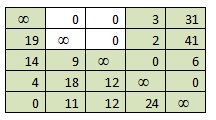
4) Элемент (2;3)=0, убираем вторую строку и третий столбец.

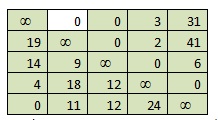
5) Остается только элемент (1;2)=0. Все.
Итого, получили гамильтонов цикл (5;1)(4;5)(3;4)(2;3)(1;2),

25+34+18+17+22=116 – длина пути.