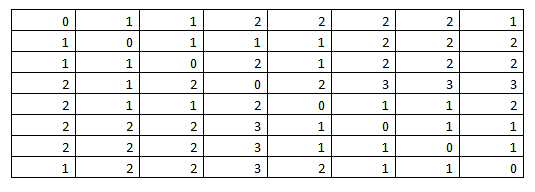
Построить матрицу метрики графа:

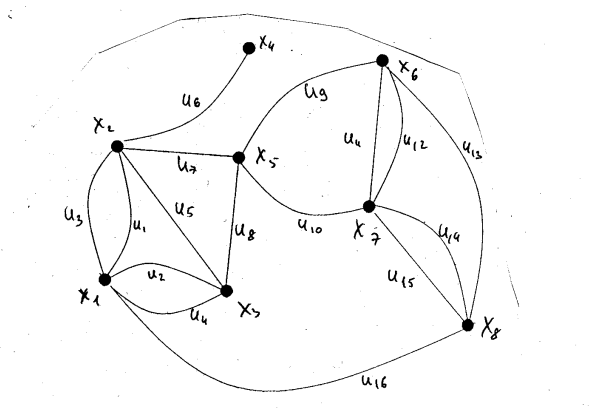
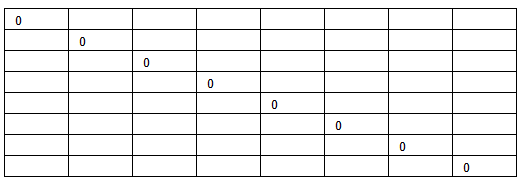
Шаг 1. Задаём матрицу метрики M . Размерность матрицы равна размерности матрицы R. Все элементы 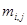матрицы M не определены.
M:
R:
S=R+E=

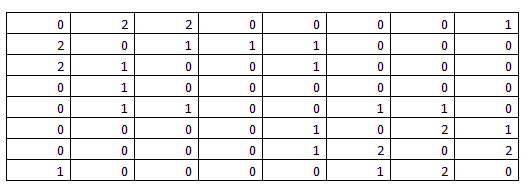
Шаг 2. Начальное значение степени k матрицы S равно «1»: k = 1. ∀ 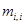присваиваем значение «0», на основании 1-ой аксиомы Фрише.

M:

Шаг 3. Всем элементам 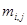, значения которых не определены, присвоить значение степени k, если соответствующие им элементы матрицы .

M:

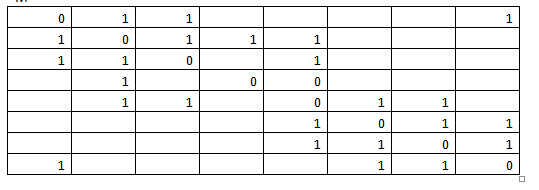
Шаг 4. Повышаем степень k матрицы S: k = k + 1, т.е. k=1+1=2

:

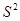
Шаг 5. Проверяем, является ли матрица 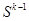устойчивой.
Т.к. 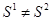, то 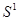не является устойчивой.
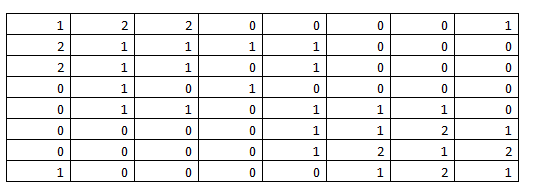
Шаг 5 (3) . Всем элементам 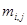, значения которых не определены, присвоить значение степени k, если соответствующие им элементы матрицы .

M:

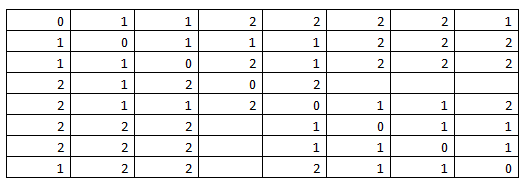
Шаг 6 (4). Повышаем степень k матрицы S: k = k + 1, т.е. k=2+1=3

:

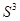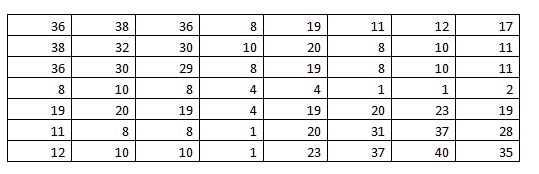
Шаг 7 (5) . Проверяем, является ли матрица 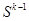устойчивой.
Т.к. 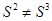, то 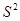не является устойчивой.
Шаг 8 (3) . Всем элементам 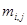, значения которых не определены, присвоить значение степени k, если соответствующие им элементы матрицы .

M:

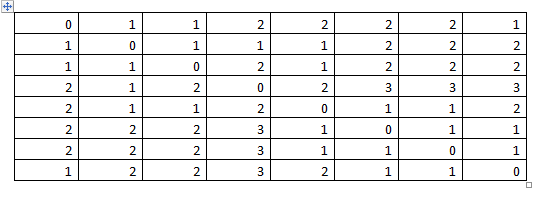
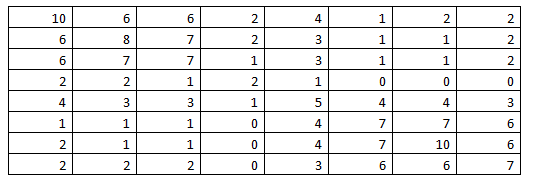
Все элементы матрицы М определены, т.е. матрица метрики графа построена:

M: