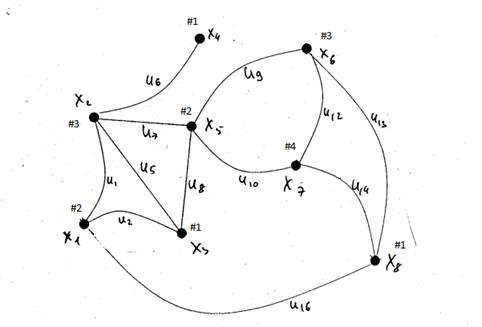
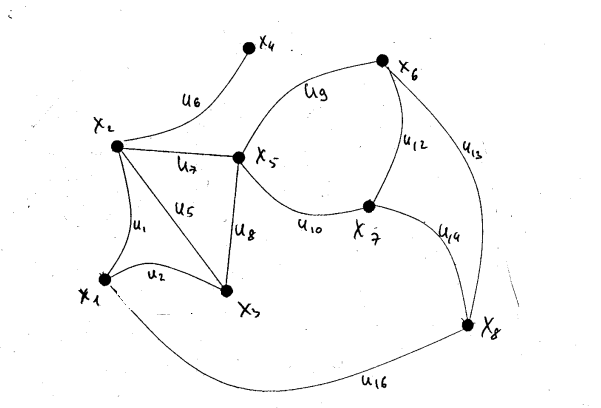
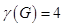С помощью алгоритма Магу—Вейсмана выполнить правильную раскраску вершин графа с минимальным количеством цветов.

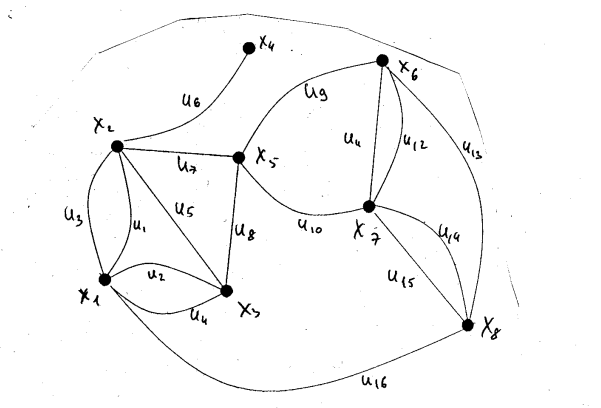
1-й этап. Находим все максимальные пустые подграфы графа G = (X , U ) с по-мощью алгоритма Магу—Вейсмана.
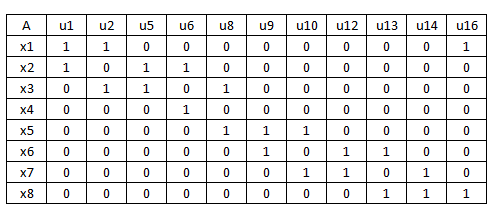
1. Составляем произведение

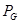
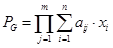
Где 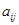— элемент матрицы инциденций графа G; 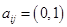, раскроем скобки и проведем преобразования по правилам алгебры логики типа: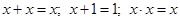

Скелет графа




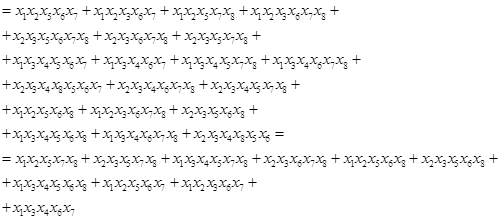
2. Для каждого слагаемого преобразованного выражения 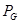запишем его дополнение до полной системы образующих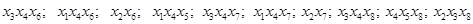

Получили полный обзор всех максимальных пустых подграфов графа G.
3-й этап. Определяем хроматическое число γ(G) графа G.
1. Упорядочим полученные множества вершин в порядке убывания их кардинальных чисел:

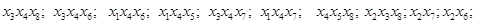
2. Припишем вершинам множества 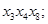цвет «1» .
3. Удалим раскрашенные вершины из всех множеств и оставшиеся множества упорядочим в порядке убывания их мощности:

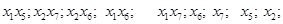
4. Припишем вершинам множества 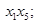цвет «2» .
5. Удалим раскрашенные вершины из всех множеств и оставшиеся множества упорядочим в порядке убывания их мощности:

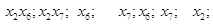
6. Припишем вершинам множества 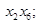цвет «3» .
7. Удалим раскрашенные вершины из всех множеств и оставшиеся множества упорядочим в порядке убывания их мощности: 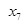и припишем ему цвет «4».
Всё. Хроматическое число графа: