Задача: решить задачу Коши (уравнение математической физики, уравнение в частных производных гиперболического типа)

,
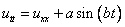
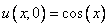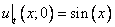
Решение:
Для уравнения вида

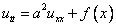
с начальными условиями
,
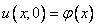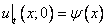
форму Даламбера имеет вид:

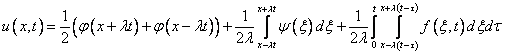
Подставим в эту формулу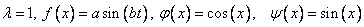

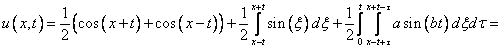
Далее следует простое интегрирование.

Ответ:
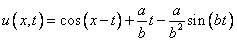
Проверка:
Конечно же решающий должен быть уверен в своих действиях, но, ради интереса, можно и провести проверку.
Итак, есть функция .
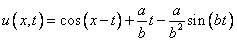Требуется проверить три факта:
1) она является решением уравнения .
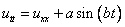Найдем вторые частные производные

Подставим в уравнение

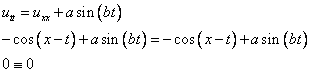
Равенство верное, т.е. эта функция является решением уравнения.
2) Проверить, что

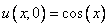
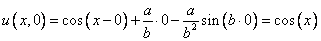
Все верно.
3) Проверить, что

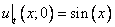
Итог: полученная функция полностью удовлетворяет условию.