Используя данные, предоставленные в таблице, проверить наличие гетероскедастичности, используя тест Голдфелда-Куандта.
| Страна | Индекс человеческого развития, Y | Суточная калорийность питания населения, ккал на душу, X |
| Дания | 0,905 | 3808 |
| Египет | 0,616 | 3289 |
| Израиль | 0,883 | 3272 |
| Индия | 0,545 | 2415 |
| Испания | 0,894 | 3295 |
| Италия | 0,900 | 3504 |
| Канада | 0,932 | 3056 |
| Казахстан | 0,740 | 3007 |
| Китай | 0,701 | 2844 |
| Латвия | 0,744 | 2861 |
| Нидерланды | 0,921 | 3259 |
| Норвегия | 0,927 | 3350 |
| Польша | 0,802 | 3344 |
| Республика Корея | 0,852 | 3336 |
| Россия | 0,747 | 2704 |
| Румыния | 0,752 | 2943 |
| США | 0,927 | 3642 |
| Турция | 0,728 | 3569 |
| Украина | 0,721 | 2753 |
| Финляндия | 0,913 | 2916 |
| Франция | 0,918 | 3551 |
| Чехия | 0,833 | 3177 |
| Швейцария | 0,914 | 3280 |
| Швеция | 0,923 | 3160 |
| ЮАР | 0,695 | 2933 |
| Япония | 0,924 | 2905 |
Упорядочим все данные по возрастанию X
| Страна | Индекс человеческого развития, Y | Суточная калорийность питания населения, ккал на душу, X |
| Индия | 0,545 | 2415 |
| Россия | 0,747 | 2704 |
| Украина | 0,721 | 2753 |
| Китай | 0,701 | 2844 |
| Латвия | 0,744 | 2861 |
| Япония | 0,924 | 2905 |
| Финляндия | 0,913 | 2916 |
| ЮАР | 0,695 | 2933 |
| Румыния | 0,752 | 2943 |
| Казахстан | 0,74 | 3007 |
| Канада | 0,932 | 3056 |
| Швеция | 0,923 | 3160 |
| Чехия | 0,833 | 3177 |
| Нидерланды | 0,921 | 3259 |
| Израиль | 0,883 | 3272 |
| Швейцария | 0,914 | 3280 |
| Египет | 0,616 | 3289 |
| Испания | 0,894 | 3295 |
| Республика Корея | 0,852 | 3336 |
| Польша | 0,802 | 3344 |
| Норвегия | 0,927 | 3350 |
| Италия | 0,9 | 3504 |
| Франция | 0,918 | 3551 |
| Турция | 0,728 | 3569 |
| США | 0,927 | 3642 |
| Дания | 0,905 | 3808 |
2) Разобьем всю выборку на 3 части размерности
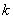 ,
, 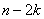 ,
, 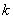 ,(т.е. первая и третья части должны содержать одинаковое количество измерений, а вторая – все, что останется), например, 9, 8 и 9.
,(т.е. первая и третья части должны содержать одинаковое количество измерений, а вторая – все, что останется), например, 9, 8 и 9.Рассмотрим первую и третью выборки
| Страна | Индекс человеческого развития,Y | Суточная калорийность питания населения, ккал на душу, X |
| Индия | 0,545 | 2415 |
| Россия | 0,747 | 2704 |
| Украина | 0,721 | 2753 |
| Китай | 0,701 | 2844 |
| Латвия | 0,744 | 2861 |
| Япония | 0,924 | 2905 |
| Финляндия | 0,913 | 2916 |
| ЮАР | 0,695 | 2933 |
| Румыния | 0,752 | 2943 |
| Испания | 0,894 | 3295 |
| Республика Корея | 0,852 | 3336 |
| Польша | 0,802 | 3344 |
| Норвегия | 0,927 | 3350 |
| Италия | 0,9 | 3504 |
| Франция | 0,918 | 3551 |
| Турция | 0,728 | 3569 |
| США | 0,927 | 3642 |
| Дания | 0,905 | 3808 |
3) Отдельно для каждой выборки построим уравнение регрессии и найдем сумму квадратов остатков
Для первой выборки
| Страна | Индекс человеческого развития,Y | Суточная калорийность питания населения, ккал на душу, X |
| Индия | 0,545 | 2415 |
| Россия | 0,747 | 2704 |
| Украина | 0,721 | 2753 |
| Китай | 0,701 | 2844 |
| Латвия | 0,744 | 2861 |
| Япония | 0,924 | 2905 |
| Финляндия | 0,913 | 2916 |
| ЮАР | 0,695 | 2933 |
| Румыния | 0,752 | 2943 |
Найдем параметры линейной регрессии
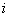 |
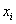 |
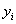 |
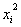 |
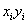 |
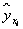 |
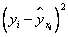 |
| 1 | 2415 | 0,545 | 5832225 | 1316,175 | 0,561824 | 0,000283 |
| 2 | 2704 | 0,747 | 7311616 | 2019,888 | 0,699471 | 0,002259 |
| 3 | 2753 | 0,721 | 7579009 | 1984,913 | 0,722809 | 3,27E-06 |
| 4 | 2844 | 0,701 | 8088336 | 1993,644 | 0,766152 | 0,004245 |
| 5 | 2861 | 0,744 | 8185321 | 2128,584 | 0,774249 | 0,000915 |
| 6 | 2905 | 0,924 | 8439025 | 2684,22 | 0,795205 | 0,016588 |
| 7 | 2916 | 0,913 | 8503056 | 2662,308 | 0,800444 | 0,012669 |
| 8 | 2933 | 0,695 | 8602489 | 2038,435 | 0,808541 | 0,012892 |
| 9 | 2943 | 0,752 | 8661249 | 2213,136 | 0,813304 | 0,003758 |
| 25274 | 6,742 | 71202326 | 19041,3 | 0,053612 |
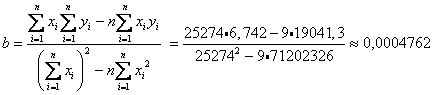
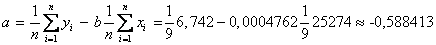
Следовательно, уравнение регрессии имеет вид
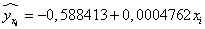
Тогда сумма квадратов остатков
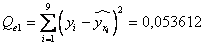
Для второй выборки
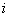 |
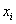 |
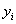 |
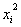 |
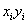 |
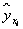 |
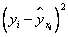 |
| 1 | 3295 | 0,894 | 10857025 | 2945,73 | 0,862752 | 0,000976 |
| 2 | 3336 | 0,852 | 11128896 | 2842,272 | 0,864826 | 0,000165 |
| 3 | 3344 | 0,802 | 11182336 | 2681,888 | 0,865231 | 0,003998 |
| 4 | 3350 | 0,927 | 11222500 | 3105,45 | 0,865534 | 0,003778 |
| 5 | 3504 | 0,9 | 12278016 | 3153,6 | 0,873326 | 0,000712 |
| 6 | 3551 | 0,918 | 12609601 | 3259,818 | 0,875704 | 0,001789 |
| 7 | 3569 | 0,728 | 12737761 | 2598,232 | 0,876614 | 0,022086 |
| 8 | 3642 | 0,927 | 13264164 | 3376,134 | 0,880308 | 0,00218 |
| 9 | 3808 | 0,905 | 14500864 | 3446,24 | 0,888706 | 0,000265 |
| 31399 | 7,853 | 109781163 | 27409,36 | 0,03595 |
Найдем параметры линейной регрессии
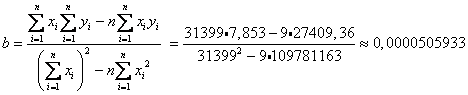
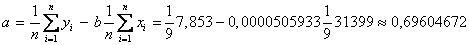
Следовательно, уравнение регрессии имеет вид
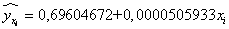
Тогда сумма квадратов остатков
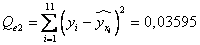
4) Сравним расчетное значение критерия 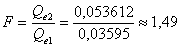 с табличным
с табличным 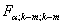 (
( 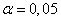 — уровень значимости,
— уровень значимости, 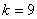 — число данных в выборке,
— число данных в выборке, 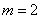 — число параметров уравнения регрессии).
— число параметров уравнения регрессии). 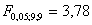 . Т.о. расчетное значение критерия меньше табличного, и следует отклонить гипотезу о наличии гетероскедастичности остатков на данном уровне значимости.
. Т.о. расчетное значение критерия меньше табличного, и следует отклонить гипотезу о наличии гетероскедастичности остатков на данном уровне значимости.


