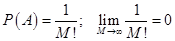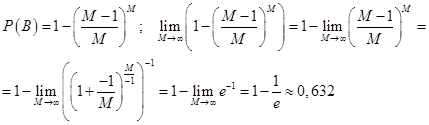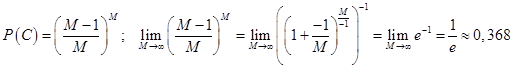11. Урна содержит 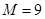занумерованных шаров с номерами от 1 до 9. Шары извлекаются по одному без возвращения. Рассматриваются следующие события:
А – номера шаров в порядке поступления образуют последовательность 1,2,…,М.
В – хотя бы один раз совпадает номер шара и порядковый номер извлечения.
С – нет ни одного совпадения номера шара и порядка извлечения.
Определить вероятность событий А,В,С. Найти предельные значения вероятностей при .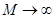
Решение:
1) Найдем вероятность события А.
Вероятность того, что первым извлечется шар с номером 1 равна 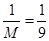(т.к. подходит только один шар с №1, а всего шаров 9 шт.) .
Вероятность того, что извлекут вторым шар с №2 равна 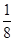, т.к. шаров всего осталось 8 шт, а походит только 1.
И т.д.
По теореме умножения вероятностей получаем:

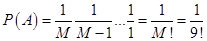
2) Найдем вероятность события В.
В – хотя бы один раз совпадает номер шара и порядковый номер извлечения.
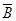— обратное событие, т.е. ни разу номер шара не совпадет с порядковым номером извлечения.
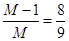— вероятность того, что первым шаром извлекут не шар с №1, т.е. всего шаров 9 шт, а подходят 8 шт.

Вычислим вероятность того, что вторым извлекут шар с номером 2.
Т.е. его не должны извлечь первым и извлечь на втором.

.
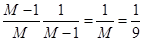Тогда, по теореме о вероятность обратного события, вероятность того, что вторым извлечется не шар №2:
.
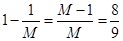Найдем вероятность того, что третьим шаром извлечется шар с №3 (т.е. его не должны извлечь при первом и втором извлечении и извлечь на третьем):

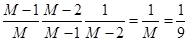
И вероятность того, что не извлекут на третьем шар с №3:

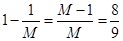
Аналогично и с другими шарами. Получили, что вероятность того, что отдельный шар будет извлечен в порядке, не соответствующим его номеру: .
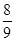Тогда вероятность того, что ни разу номер шара не совпадет с порядковым номером извлечения :

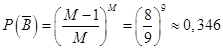
Значите:
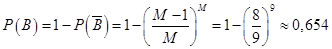
3)
Найдем вероятность события С – нет ни одного совпадения номера шара и порядка извлечения.
События С и 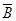совпадают, т.е.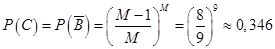
4) Найдем значения предельных вероятностей при .
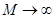