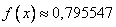Замечание: подробные вычисления не приводятся, их легко проверить при помощи Excel,, если конечно вы умеете умножать там матрицы и находить обратные. Используются округления чисел с запасом, до 5-го или 6-го знака после запятой, но это лишь запись чисел потому, что вычисления производятся Excel’ем, т.е. с гораздо большей точностью, чем необходимая.

Задача:

Минимизировать функцию 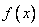методом Ньютона до момента достижения точности
.

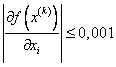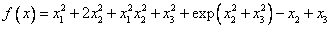
Решение:
Итак: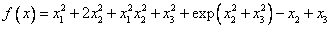
Суть метода:
Итерационная формула метода Ньютона для минимизации функции трех переменных имеет вид:
.
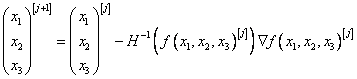Найдем градиент и матрицу Гессе функции
.

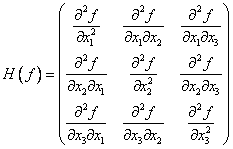Составим градиент



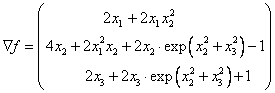
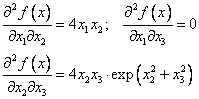
Составим матрицу Гессе

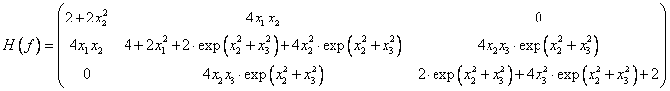
Начнем.
Первая итерация. Пусть

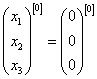
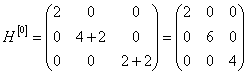
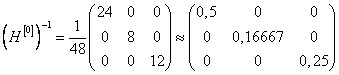
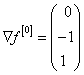
Подставим


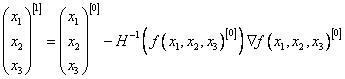
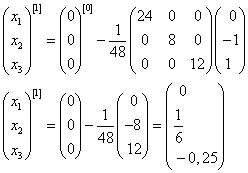
Проверим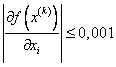

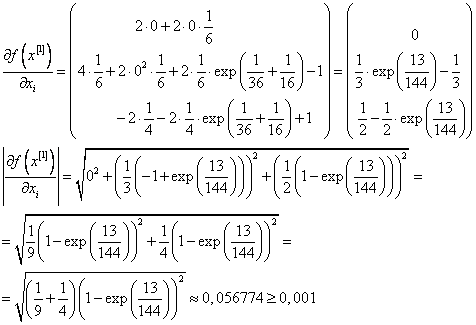
Сделаем вторую итерацию.




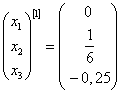
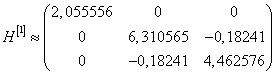
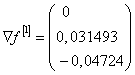
Подставим


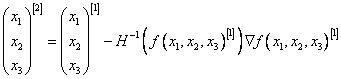
Проверим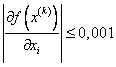

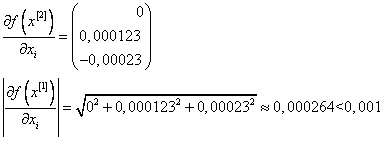
Необходимое условие выполнено

Ответ: 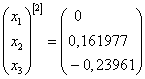;