.
Условие производственной задачи:
, 
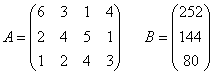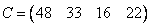
Постановка двойственной задачи:
Предположим, что нам предложено продать ресурсы, используемые на нашем производстве. Требуется вычислить оптимальные цены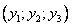 
на ресурсы.
Для производства продукции первого типа требуется 6 единиц ресурсов первого типа, 2 единицы ресурса второго типа и 1 единица ресурса третьего типа (об этом говорят элементы первого столбца матрицы).
При установленных ценах 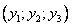затраты на единицу продукции первого типа составят:
денежных единиц.
Но за единицу продукции первого типа при продаже можно получить 48 дн.ед. Т.е. продажа ресурсов не должна быть убыточнее производства изделия и продажи его.
.
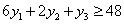Составим аналогичные неравенства для продукции остальных типов.
При этом за все имеющиеся ресурсы можно выручить 
Итог постановки:
Найти вектор двойственных оценок 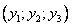, минимизирующий общую оценку всех ресурсов: 
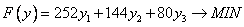при условии, что по каждому виду продукции суммарная оценка всех ресурсов, затрачиваемых на производство единицы продукции, не меньше прибыли, получаемой от реализации единицы этой продукции, это ограничение задается системой неравенств:
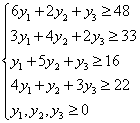
Для решения этой задачи используем вторую основную теорему двойственности, согласно которой для оптимальности допустимых решений 
и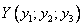 
пары двойственных задач необходимо и достаточно выполнение условий
и 
Ранее было найдено, что
Система примет вид
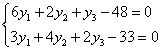
Учтем, что третий ресурс был избыточным, т.к.
, то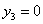 
. Система уравнений приняла вид: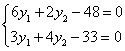
Решим эту систему уравнений:
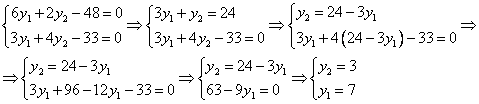
Итог: 
Общая минимальная оценка 
.