Решить начально-краевую задачу для неоднородного волнового уравнения
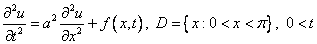
С однородными граничными и начальными условиями
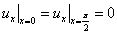
Решение: решим вспомогательную задачу Штурма-Лиувилля, которая получается в результате разделения переменных в однородном уравнении
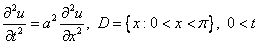
С однородными граничными условиями
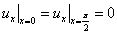
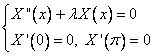
Пример решения аналогичного уравнения можно посмотреть здесь.
Собственные значения этого уравнения при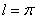 
: 
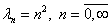
Собственные функции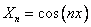 
.
Решение исходной задачи будем искать в виде разложения в функциональный ряд по собственным функциям с неизвестными коэффициентами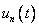 
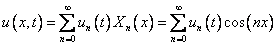
предполагая, что его можно дважды дифференцировать по переменной х и дважды по переменной t.
Разложим функции
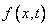, в ряд по собственным функциям
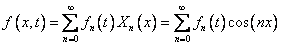
Разложим остальные функции в ряд по собственным функциям
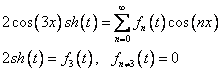
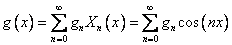
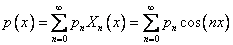
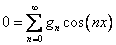
Подставим полученные выражения
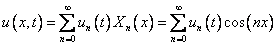
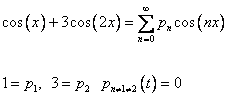
в исходное уравнение
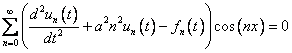
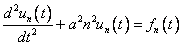
Подставим
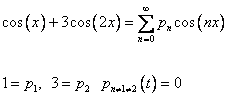
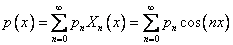
В начальное условие
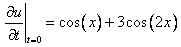
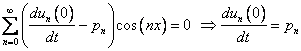
Учтем, что
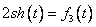
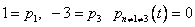
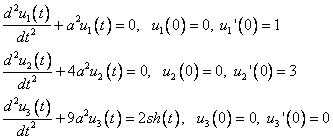
Решаем по очереди
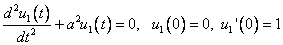
И второе
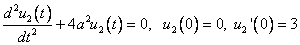
Далее
Подставим найденные значения функций и получим ответ:
