1. Бросаются две игральные кости. Определить вероятность того, что
а) сумма числа очков не превосходит числа 15;
б) произведение числа очков не превосходит числа 15;
в) произведение числа очков делится на 15.
Решение:
Будем решать эту задачу с помощью классического определения вероятности.
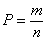 , где
, где
n- количество всевозможных исходов.
m- количество благоприятных исходов.
Распишем всевозможные исходы эксперимента. Например (2,4) будет означать, что на первой кости выпала 2, а на второй 4.
| (1,1) | (2,1) | (3,1) | (4,1) | (5,1) | (6,1) |
| (1,2) | (2,2) | (3,2) | (4,2) | (5,2) | (6,2) |
| (1,3) | (2,3) | (3,3) | (4,3) | (5,3) | (6,3) |
| (1,4) | (2,4) | (3,4) | (4,4) | (5,4) | (6,4) |
| (1,5) | (2,5) | (3,5) | (4,5) | (5,5) | (6,5) |
| (1,6) | (2,6) | (3,6) | (4,5) | (5,6) | (6,6) |
Всего – 36 вариантов, т.е. n=36.
А) сумма числа очков не превосходит числа 15. Вообще то сумма на двух костях может быть максимум равна 12, т.е. подходят все пары, т.е. m=36.
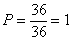
б) произведение числа очков не превосходит числа 15. Подходят пары :
| (1,1)* | (2,1)* | (3,1)* | (4,1)* | (5,1)* | (6,1)* |
| (1,2)* | (2,2)* | (3,2)* | (4,2)* | (5,2)* | (6,2)* |
| (1,3)* | (2,3)* | (3,3)* | (4,3)* | (5,3) | (6,3) |
| (1,4)* | (2,4)* | (3,4)* | (4,4) | (5,4) | (6,4) |
| (1,5)* | (2,5)* | (3,5) | (4,5) | (5,5) | (6,5) |
| (1,6)* | (2,6)* | (3,6) | (4,5) | (5,6) | (6,6) |
Т.е. 23 пары. m = 23.
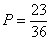
в) произведение числа очков делится на 15. Т.е. это, например, числа 15,30,45, и т.д.
Пары, произведение в которых равно этим цифрам это :
| (1,1) | (2,1) | (3,1) | (4,1) | (5,1) | (6,1) |
| (1,2) | (2,2) | (3,2) | (4,2) | (5,2) | (6,2) |
| (1,3) | (2,3) | (3,3) | (4,3) | (5,3)* | (6,3) |
| (1,4) | (2,4) | (3,4) | (4,4) | (5,4) | (6,4) |
| (1,5) | (2,5) | (3,5)* | (4,5) | (5,5) | (6,5)* |
| (1,6) | (2,6) | (3,6) | (4,5) | (5,6)* | (6,6) |
Т.е., в данном случае m=4
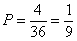
Ответ: а) 1 б) 23/36 в) 1/9
2. Имеются изделия четырех сортов, причем число изделий каждого сорта равно, соответственно, 2,5,2,3. Для контроля наудачу берутся 7 изделий. Определить вероятность того, что среди них 1 первосортная деталь, 3 – второго сорта, 1 – третьего, 2 – четвертого сорта.
Решение:
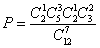 ,
,
где 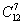 — количество способов, которыми из всех 12 деталей можно выбрать любые 7.
— количество способов, которыми из всех 12 деталей можно выбрать любые 7.
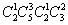 — это количество способов, которыми из 2 деталей первого сорта можно выбрать 1, из 5 деталей второго сорта выбрать 3, и т.д.
— это количество способов, которыми из 2 деталей первого сорта можно выбрать 1, из 5 деталей второго сорта выбрать 3, и т.д.
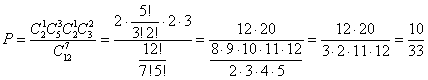 .
.
Ответ: 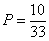 .
.
3. Среди 8 лотерейных билетов 4 выигрышных. Наудачу взяли 3 билета. Определить вероятность того, что среди них 2 выигрышных.
Решение:
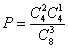 ,
,
где 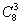 -количество способов выбора из всех 8-ми билетов любых 3-х.
-количество способов выбора из всех 8-ми билетов любых 3-х.
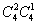 — количество способов выбора из 4-х выигрышных любых 2-х и из 4-х невыигрышных оставшегося 1-го.
— количество способов выбора из 4-х выигрышных любых 2-х и из 4-х невыигрышных оставшегося 1-го.
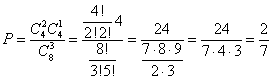
Ответ: 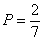 .
.
4. В лифт 10-ти этажного дома сели 6 пассажиров. Каждый независимо от других с одинаковой вероятностью может выйти на любом (начиная со второго) этаже. Определить вероятность того, что:
а) все вышли на разных этажах;
б) по крайней мере, двое сошли на одном этаже.
Решение:
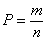 .
.
n- количество способов, которыми все люди могут выйти на любых этажах.
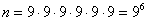 , т.к. каждый из 6-ти человек может выйти на любом из 9-ти имеющихся в доме этажей, т.к. на первом они не выходят.
, т.к. каждый из 6-ти человек может выйти на любом из 9-ти имеющихся в доме этажей, т.к. на первом они не выходят.
А) все вышли на разных этажах.
m-количество способов выходя людей так, чтобы ни на одном этаже не вышли 2 человека.
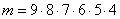 , т.к., допустим, первый человек может выйти на любом из девяти этажей, у второго выбор уже на 1 этаж меньше, т.е. 8 вариантов, т.к. на одном этаже первый уже вышел, у третьего пассажира осталось для выхода всего 7 этажей и т.д.
, т.к., допустим, первый человек может выйти на любом из девяти этажей, у второго выбор уже на 1 этаж меньше, т.е. 8 вариантов, т.к. на одном этаже первый уже вышел, у третьего пассажира осталось для выхода всего 7 этажей и т.д.
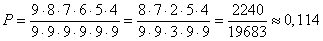 .
.
Б) по крайней мере, двое сошли на одном этаже.
Событие «по крайней мере, двое сошли на одном этаже» противоположно событию «все сошли на разных этажах». Воспользуемся формулой вероятности противоположного события
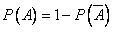
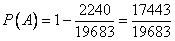
Ответ: 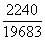 ,
, 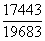 .
.
5. В отрезке единичной длины наудачу появляется точка. Определить вероятность того, что расстояние от точки до концов отрезка превосходит величину ¼.
Решение: Задача решается с помощью формулы геометрической вероятности.
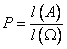
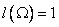 — вся длина, на которую может попасть точка.
— вся длина, на которую может попасть точка.
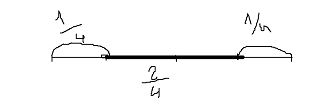
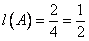 -длина отрезка, попадание на который выгодно, т.е. необходимо, чтобы расстояние от точки до концов отрезка было не меньше ¼.
-длина отрезка, попадание на который выгодно, т.е. необходимо, чтобы расстояние от точки до концов отрезка было не меньше ¼.
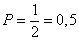
Ответ: 0,5.
15. В магазин поступают однотипные изделия с трех заводов, причем первый завод поставляет 50% изделий, второй завод – 20%, третий завод – 30%. Среди изделий 1-го завода 90% первосортных, среди изделий 2-го – 80%, 3-го – 90%. Куплено одно изделие, оно оказалось первосортным. Определить вероятность того, что изделие выпущено 3-м заводом.
Решение:
Воспользуемся формулой Байеса.
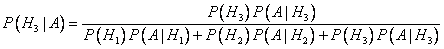
Перечислим гипотезы:
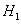 — деталь поступила с первого завода,
— деталь поступила с первого завода, 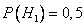
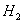 — деталь поступила с первого завода,
— деталь поступила с первого завода, 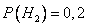
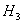 — деталь поступила с первого завода,
— деталь поступила с первого завода, 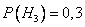 .
.
Найдем условные вероятности:
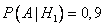 — вероятность того, что деталь, доставленная с первого завода, первосортная.
— вероятность того, что деталь, доставленная с первого завода, первосортная.
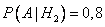 — вероятность того, что деталь со второго завода, первосортная.
— вероятность того, что деталь со второго завода, первосортная.
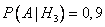 — вероятность того, что деталь с третьего завода, первосортная.
— вероятность того, что деталь с третьего завода, первосортная.
Подставим:
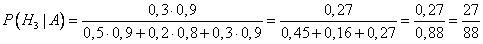
Ответ: 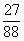 .
.
21. Дана плотность распределения 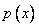 случайно величины
случайно величины  . Найти параметр
. Найти параметр  , математическое ожидание
, математическое ожидание  , дисперсию
, дисперсию  , функцию распределения случайной величины
, функцию распределения случайной величины  , вероятность выполнения неравенства
, вероятность выполнения неравенства  .
.
 .
.
Решение:
1) Для нахождения параметра  воспользуемся свойством плотности распределения:
воспользуемся свойством плотности распределения:


Плотность распределения принимает вид:
 .
.
2) Найдем  по формуле
по формуле 

3) Найдем  по формуле
по формуле 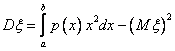

4) Найдем функцию распределения случайной величины  .
.
Воспользуемся формулой  .
.
А) Пусть  ,
,  ,
,

б) Пусть  ,
,  ,
,

в) Пусть 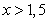 ,
,  ,
,
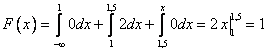
Итак, функция распределения имеет вид:

г) Найдем вероятность выполнения неравенства  .
.
Воспользуемся формулой
 .
.
22. Плотность распределения вероятностей случайной величины  имеет вид
имеет вид 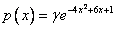 . Найти параметр
. Найти параметр  , математическое ожидание
, математическое ожидание  , дисперсию
, дисперсию  , функцию распределения случайной величины
, функцию распределения случайной величины  , вероятность выполнения неравенства
, вероятность выполнения неравенства 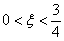 .
.
Решение:
1) Для нахождения параметра  воспользуемся свойством плотности распределения:
воспользуемся свойством плотности распределения:


Плотность распределения принимает вид:

— Нормальное распределение с параметрами 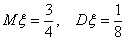 ,
,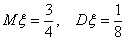
4) Найдем функцию распределения случайной величины  .
.
Воспользуемся формулой  .
.
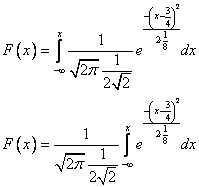
г) Найдем вероятность выполнения неравенства 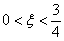 .
.
Воспользуемся формулой

23. По данному закону распределения случайной величины найти характеристическую функцию 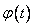 , математическое ожидание
, математическое ожидание  , дисперсию
, дисперсию  случайной величины
случайной величины  .
.
Решение:
Дан закон Пуассона: 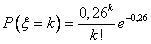 .
.
Найдем характеристическую функцию.
Воспользуемся формулой
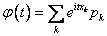 .
.
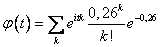 .
.
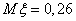 ,
, 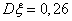 . (т.к. дан именно закон Пуассона, а про него известно, что числовые характеристики равны а, в данном варианте a = 0,26.)
. (т.к. дан именно закон Пуассона, а про него известно, что числовые характеристики равны а, в данном варианте a = 0,26.)
36. Случайная величина  имеет нормальное распределение с неизвестным математическим ожиданием
имеет нормальное распределение с неизвестным математическим ожиданием  и известной дисперсией
и известной дисперсией  . По выборке
. По выборке 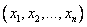 объема вычислено выборочное среднее
объема вычислено выборочное среднее 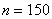 . Определить доверительный интервал для неизвестного параметра распределения
. Определить доверительный интервал для неизвестного параметра распределения  , отвечающий заданной доверительной вероятности
, отвечающий заданной доверительной вероятности  .
.
Решение:
Воспользуемся формулой:
 , где
, где

— табличные данные.
Подставляем в неравенство.

Ответ: 


