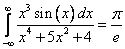Все интегралы вычисляются с использованием Леммы Жордана:
Пусть 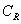 — лежащая в верхней полуплоскости дуга окружности радиуса R с центром в некоторой фиксированной точке
— лежащая в верхней полуплоскости дуга окружности радиуса R с центром в некоторой фиксированной точке 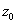 , а функция
, а функция 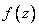 имеет вид:
имеет вид:
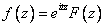 , причем
, причем 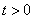 . Если функция
. Если функция 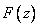 аналитична на действительной оси, а в верхней полуплоскости имеет конечное число особых точек и
аналитична на действительной оси, а в верхней полуплоскости имеет конечное число особых точек и 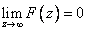 , то
, то
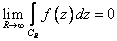 .
.
Но это определение, а при решении задач используется формула:
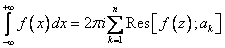 .
.
Замечание:
Если функция дифференцируема не только в данной точке, но и в некоторой окрестности этой точки, то она называется аналитической в этой точке.
Пояснение на пальцах: аналитическая в области – от нее можно вычислить производную в любой точке этой области.
Так же помним про формулу Эйлера:
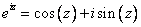
1.
Вычислить интеграл:
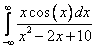 .
.
Вычислим значение вспомогательного интеграла 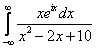 .
.
По лемме Жордана 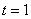 ,
, 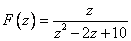
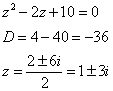
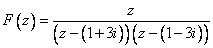 — аналитична на действительной оси.
— аналитична на действительной оси. 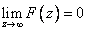
Условия леммы Жордана выполнены.
Функция 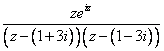 имеет особыми точками полюсы первого порядка
имеет особыми точками полюсы первого порядка 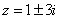 . В верхней полуплоскости лежит только
. В верхней полуплоскости лежит только 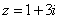 . Найдем вычет в этой точке:
. Найдем вычет в этой точке:
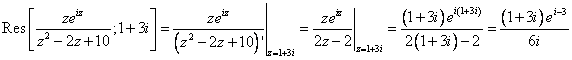
Пользуемся 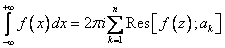
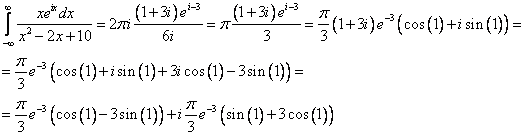
По формуле Эйлера (см выше).
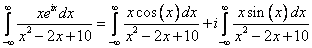
Приравняем действительные части последних двух выражений:
Ответ: 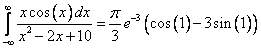
2.
Вычислить интеграл:
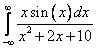 .
.
Вычислим значение вспомогательного интеграла 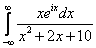 .
.
По лемме Жордана 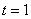 ,
, 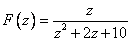
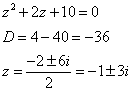
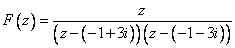 — аналитична на действительной оси.
— аналитична на действительной оси.
Условия леммы Жордана выполнены.
Функция 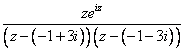 имеет особыми точками полюсы первого порядка
имеет особыми точками полюсы первого порядка 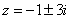 . В верхней полуплоскости лежит только
. В верхней полуплоскости лежит только 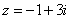 . Найдем вычет в этой точке:
. Найдем вычет в этой точке:
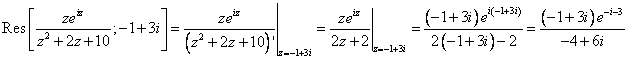
Пользуемся 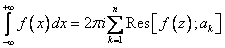

По формуле Эйлера (см выше).

Приравняем мнимые части последних двух выражений.
Ответ: 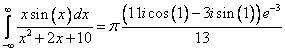
3.
Вычислить интеграл:
 .
.
Вычислим значение вспомогательного интеграла 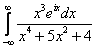 .
.
По лемме Жордана 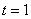 ,
, 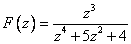
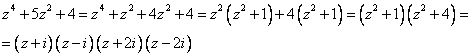
 — аналитична на действительной оси.
— аналитична на действительной оси. 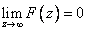
Условия леммы Жордана выполнены.
Функция  имеет особыми точками полюсы первого порядка
имеет особыми точками полюсы первого порядка 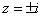 и
и 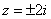 . В верхней полуплоскости лежит
. В верхней полуплоскости лежит 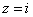 и
и 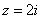 . Найдем вычеты в этой точке:
. Найдем вычеты в этой точке:

Пользуемся 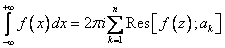
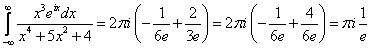
По формуле Эйлера (см выше).
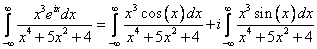
Приравняем мнимые части последних двух выражений
Ответ: